算法常用的解题思路---双指针（Double Pointer）

Posted by Sunfy on 2021-07-22
Words 7.4k and Reading Time 30 Minutes
Viewed Times
Viewed Times
Visitors In Total

什么是双指针（对撞指针、快慢指针）

双指针，指的是在遍历对象的过程中，不是普通的使用单个指针进行访问，而是使用两个相同方向（快慢指针）或者相反方向（对撞指针）的指针进行扫描，从而达到相应的目的。

换言之，双指针法充分使用了数组有序这一特征，从而在某些情况下能够简化一些运算。

977. 有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
示例 1：
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：
输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序

方法一：直接排序

思路与算法

最简单的方法就是将数组 nums 中的数平方后直接排序。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int[] sortedSquares(int[] nums) {
        // 直接遍历求积排序
        int[] ans = new int[nums.length];
        for (int i = 0; i< nums.length; i++) {
            ans[i] = nums[i] * nums[i];
        }
        Arrays.sort(ans);
        return ans;
	}
}

复杂度分析

  • 时间复杂度：O(nlogn)，其中n 是数组 nums 的长度。
  • 空间复杂度：O(logn)。除了存储答案的数组以外，我们需要O(logn) 的栈空间进行排序。

方法二：双指针

思路与算法

方法一没有利用「数组 nums已经按照升序排序」这个条件。显然，如果数组 nums中的所有数都是非负数，那么将每个数平方后，数组仍然保持升序；如果数组 nums中的所有数都是负数，那么将每个数平方后，数组会保持降序。

这样一来，如果我们能够找到数组 nums中负数与非负数的分界线，那么就可以用类似「归并排序」的方法了。具体地，我们设 neg 为数组 nums中负数与非负数的分界线，也就是说，nums[0] 到 nums[neg] 均为负数，而nums[neg+1] 到 nums[n−1] 均为非负数。当我们将数组 nums中的数平方后，那么nums[0] 到 nums[neg] 单调递减，nums[neg+1] 到 nums[n−1] 单调递增。

由于我们得到了两个已经有序的子数组，因此就可以使用归并的方法进行排序了。具体地，使用两个指针分别指向位置 neg 和 neg+1，每次比较两个指针对应的数，选择较小的那个放入答案并移动指针。当某一指针移至边界时，将另一指针还未遍历到的数依次放入答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public int[] sortedSquares2(int[] nums) {
        // 双指针
        // 获得正负数分界
        int boundaries = -1;
        int numsLength = nums.length;
        for (int i = 0; i < numsLength; i++) {
            if (nums[i] < 0) {
                boundaries = i;
            } else {
                break;
            }
        }

        int[] ans = new int[numsLength];
        // 从正负分界点定义双指针（正负分界点采用的是第一个负数的索引，加1表示第一个非负数的位置）
        int index = 0, i = boundaries, j = boundaries + 1;
        // 循环条件 [i--0]  索引区间表示所有负数的区间 [j--numsLength) 表示所有非负数的区间
        while (i>= 0 || j<numsLength) {
            // i<0 说明遍历过程中，所有负数都已经遍历完，将所有剩下的非负数直接写入数组
            if (i < 0) {
                ans[index] = nums[j] * nums[j];
                j++;
            } else if (j == numsLength) {
                // j == numsLength 说明所有的正数都遍历完成，则将所有的负数乘积后写入数组
                ans[index] = nums[i] * nums[i];
                i--;
            } else if(nums[i] * nums[i] < nums[j] * nums[j]){
                ans[index] = nums[i] * nums[i];
                i--;
            } else {
                ans[index] = nums[j] * nums[j];
                j++;
            }
            index++;
        }
        return ans;
    }
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 是数组nums 的长度。
  • 空间复杂度：O(1)。除了存储答案的数组以外，我们只需要维护常量空间。

方法三：双指针

思路与算法

同样地，我们可以使用两个指针分别指向位置 0 和 n−1，每次比较两个指针对应的数，选择较大的那个逆序放入答案并移动指针。这种方法无需处理某一指针移动至边界的情况，读者可以仔细思考其精髓所在。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int[] sortedSquares3(int[] nums) {
        // 双指针2
        int numsLength = nums.length;
        int[] ans = new int[numsLength];
        // 对撞指针
        // i 递增  j 递减
        // 逐个进行比较，直接写入目标数组
        for (int i = 0, j = numsLength-1, pos = numsLength-1; i <= j;) {
            if (nums[i] * nums[i] > nums[j] * nums[j]) {
                ans[pos] = nums[i] * nums[i];
                i++;
            } else {
                ans[pos] = nums[j] * nums[j];
                j--;
            }
            pos--;
        }
        return ans;
    }
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 是数组nums 的长度。
  • 空间复杂度：O(1)。除了存储答案的数组以外，我们只需要维护常量空间。

189. 旋转数组

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

进阶：

尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]

示例 2:
输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]

提示：a
1 <= nums.length <= 2 * 104
-231 <= nums[i] <= 231 - 1
0 <= k <= 105

方法一：使用额外的数组

我们可以使用额外的数组来将每个元素放至正确的位置。用 n 表示数组的长度，我们遍历原数组，将原数组下标为 i 的元素放至新数组下标为 (i+k)mod n 的位置，最后将新数组拷贝至原数组即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public void rotate(int[] nums, int k) {
        System.out.println(Arrays.toString(nums));
        int n = nums.length;
        int[] ans = new int[n];
        for (int i = 0; i < n; i++) {
            // 移动步长+当前索引 取模数组长度 得到当前元素应该存放的位置
            ans[(i + k) % n] = nums[i];
        }
        System.arraycopy(ans, 0, nums, 0, n);
        System.out.println(Arrays.toString(ans));
    }
}

复杂度分析

  • 时间复杂度： O(n)，其中 n 为数组的长度。
  • 空间复杂度： O(n)。

方法二：环状替换

image-20210722114537589

1
2
nums = [1, 2, 3, 4, 5, 6]
k = 2

image-20210722114626685

如果读者对上面的数学推导的理解有一定困难，也可以使用另外一种方式完成代码：使用单独的变量count 跟踪当前已经访问的元素数量，当 count=n 时，结束遍历过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public void rotate1(int[] nums, int k) {
        int n = nums.length;
        k = k % n;
        // 取得移动步长和总数组长度的最大公约数
        int count = gcd(k, n);
        for (int start = 0; start < count; start++) {
            // 记录开始的位置和开始位置元素
            int current = start;
            int prev = nums[start];
            do {
                // 根据移动步长确定下一个移动位置
                int next = (current + k) % n;
                // 暂存下一个移动位置元素
                int temp = nums[next];
                nums[next] = prev; // 将正在移动的元素放入下一个步长位置
                prev = temp; // 将下一个步长原有元素替暂存起来
                current = next; // 将下一个步长的元素索引暂存
            } while (start != current);
        }
        System.out.println(Arrays.toString(nums));
    }

    // 求最大公约数
    public int gcd(int x, int y) {
        return y > 0 ? gcd(y, x % y) : x;
    }
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 为数组的长度。每个元素只会被遍历一次。
  • 空间复杂度：O(1)。我们只需常数空间存放若干变量。

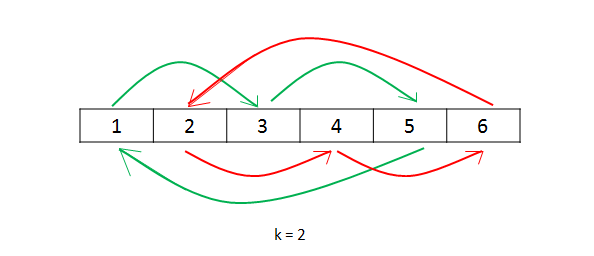
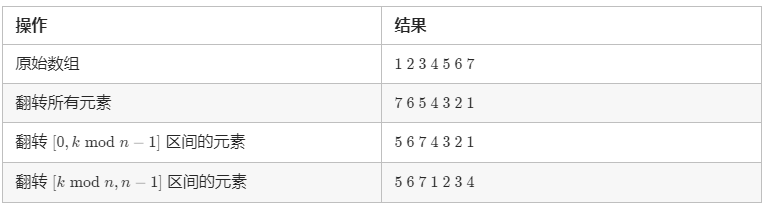
方法三：数组翻转

该方法基于如下的事实：当我们将数组的元素向右移动 k 次后，尾部 k mod n 个元素会移动至数组头部，其余元素向后移动 k mod n 个位置。

该方法为数组的翻转：我们可以先将所有元素翻转，这样尾部的 k mod n 个元素就被移至数组头部，然后我们再翻转[0, k mod n −1] 区间的元素和 [k mod n,n−1] 区间的元素即能得到最后的答案。

我们以 n=7，k=3 为例进行如下展示：

image-20210722115109442

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public void rotate2(int[] nums, int k) {
        k %= nums.length;
        // 将数组整体倒转
        reverse(nums, 0, nums.length-1);
        // 将数组前移部分数据进行倒装
        reverse(nums, 0, k-1);
        // 将数组原数据后移部分倒装
        reverse(nums, k, nums.length -1);
        System.out.println(Arrays.toString(nums));
    }

    // 封装数组倒转方法
    public void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int tem = nums[start];
            nums[start] = nums[end];
            nums[end] = tem;
            start++;
            end--;
        }
    }
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 为数组的长度。每个元素被翻转两次，一共 n 个元素，因此总时间复杂度为 O(2n)=O(n)。
  • 空间复杂度：O(1)。

283. 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

1
2
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]

说明:

  1. 必须在原数组上操作，不能拷贝额外的数组。
  2. 尽量减少操作次数。

方法：双指针

思路及解法

使用双指针，左指针指向当前已经处理好的序列的尾部，右指针指向待处理序列的头部。

右指针不断向右移动，每次右指针指向非零数，则将左右指针对应的数交换，同时左指针右移。

注意到以下性质：

  1. 左指针左边均为非零数；

  2. 右指针左边直到左指针处均为零。

因此每次交换，都是将左指针的零与右指针的非零数交换，且非零数的相对顺序并未改变。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public void moveZeroes(int[] nums) {
        int n = nums.length, left = 0, right = 0;
        while (right < n) {
            if (nums[right] != 0) {
                int temp = nums[left];
                nums[left] = nums[right];
                nums[right] = temp;
                left++;
            }
            right++;
        }
        System.out.println(Arrays.toString(nums));
    }
}

复杂度分析

  • 时间复杂度：O(n)，其中 n为序列长度。每个位置至多被遍历两次。
  • 空间复杂度：O(1)。只需要常数的空间存放若干变量。

167. 两数之和 II - 输入有序数组

给定一个已按照 升序排列 的整数数组 numbers ，请你从数组中找出两个数满足相加之和等于目标数 target 。

函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ，所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length。

你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

1
2
3
4
5
6
7
8
9
10
11
12
示例 1：
输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

示例 2：
输入：numbers = [2,3,4], target = 6
输出：[1,3]

示例 3：
输入：numbers = [-1,0], target = -1
输出：[1,2]

方法一:双循环

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int n = numbers.length;
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < n; j++) {
                // 基于条件两个数值不能相同，相同时跳出
                if(i == j) continue;
                // 根据i的每个值内容遍历每个j判断是否满足条件
                if(numbers[i] + numbers[j] == target) return new int[]{i+1, j+1};
            }
        }
        return new int[]{};
    }
}

方法二：二分查找

在数组中找到两个数，使得它们的和等于目标值，可以首先固定第一个数，然后寻找第二个数，第二个数等于目标值减去第一个数的差。利用数组的有序性质，可以通过二分查找的方法寻找第二个数。为了避免重复寻找，在寻找第二个数时，只在第一个数的右侧寻找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    // 二分查找
    public int[] twoSum1(int[] numbers, int target) {
        int n = numbers.length;
        for (int i = 0; i < n; i++) {
            // 二分查找目标值
            int find = target - numbers[i];
            // 因为提供数组为有序数组，可以采用二分查找进行查找
            int mid, left = i + 1, right = n - 1;
            while (left <= right) {
                mid = left + (right - left) / 2;
                if (find == numbers[mid]) {
                    return new int[]{i + 1, mid + 1};
                } else if (numbers[mid] < find) {
                    left = mid + 1;
                } else {
                    right = mid - 1;
                }
            }
        }
        return new int[]{-1, -1};
    }
}

复杂度分析

  • 时间复杂度：O(nlogn)，其中 n 是数组的长度。需要遍历数组一次确定第一个数，时间复杂度是 O(n)，寻找第二个数使用二分查找，时间复杂度是O(logn)，因此总时间复杂度是 O(nlogn)。
  • 空间复杂度：O(1)。

方法二：双指针

初始时两个指针分别指向第一个元素位置和最后一个元素的位置。每次计算两个指针指向的两个元素之和，并和目标值比较。如果两个元素之和等于目标值，则发现了唯一解。如果两个元素之和小于目标值，则将左侧指针右移一位。如果两个元素之和大于目标值，则将右侧指针左移一位。移动指针之后，重复上述操作，直到找到答案。

使用双指针的实质是缩小查找范围。那么会不会把可能的解过滤掉？答案是不会。假设 numbers[i]+numbers[j]=target 是唯一解，其中 0≤i<j≤numbers.length−1。初始时两个指针分别指向下标 00 和下标 numbers.length−1，左指针指向的下标小于或等于 i，右指针指向的下标大于或等于 j。除非初始时左指针和右指针已经位于下标 i 和 j，否则一定是左指针先到达下标 ii 的位置或者右指针先到达下标 j 的位置。

如果左指针先到达下标 ii 的位置，此时右指针还在下标 j 的右侧，sum>target，因此一定是右指针左移，左指针不可能移到 i 的右侧。

如果右指针先到达下标 j 的位置，此时左指针还在下标 i 的左侧，sum<target，因此一定是左指针右移，右指针不可能移到 j 的左侧。

由此可见，在整个移动过程中，左指针不可能移到 ii 的右侧，右指针不可能移到 j 的左侧，因此不会把可能的解过滤掉。由于题目确保有唯一的答案，因此使用双指针一定可以找到答案。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    // 双指针
    public int[] twoSum2(int[] numbers, int target) {
        int left = 0, right = numbers.length - 1;
        while (left < right) {
            // 双指针查找目标值
            int find = numbers[left] + numbers[right];
            if(find == target) {
                return new int[]{left+1, right+1};
            } else if(find < target){
                left++;
            } else {
                right--;
            }
        }
        return new int[]{-1, -1};
    }
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 是数组的长度。两个指针移动的总次数最多为 n次。
  • 空间复杂度：O(1)。

344. 反转字符串

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。

1
2
3
4
5
6
7
示例 1：
输入：["h","e","l","l","o"]
输出：["o","l","l","e","h"]

示例 2：
输入：["H","a","n","n","a","h"]
输出：["h","a","n","n","a","H"]

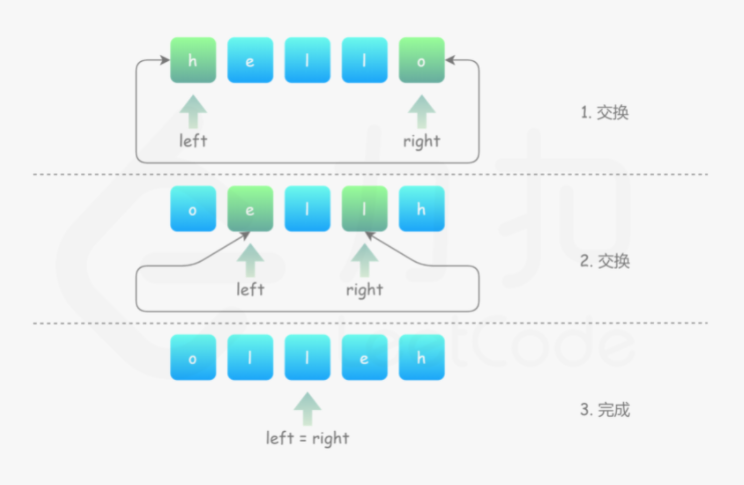
方法：双指针

思路与算法

对于长度为 N 的待被反转的字符数组，我们可以观察反转前后下标的变化，假设反转前字符数组为 s[0] s[1] s[2] ... s[N - 1]，那么反转后字符数组为 s[N - 1] s[N - 2] ... s[0]。比较反转前后下标变化很容易得出 s[i] 的字符与 s[N - 1 - i] 的字符发生了交换的规律，因此我们可以得出如下双指针的解法：

  • 将 left 指向字符数组首元素，right 指向字符数组尾元素。
  • 当 left < right：
    • 交换 s[left] 和 s[right]；
    • left 指针右移一位，即 left = left + 1；
    • right 指针左移一位，即 right = right - 1。
  • 当 left >= right，反转结束，返回字符数组即可。

image-20210724105633509

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public void reverseString(char[] s) {
        int left = 0, right = s.length-1;
        while(left <= right){
            char tmp = s[left];
            s[left] = s[right];
            s[right] = tmp;
            left++;
            right--;
        }
    }
}

// for循环
class Solution {
    public void reverseString(char[] s) {
        int n = s.length;
        for (int left = 0, right = n - 1; left < right; ++left, --right) {
            char tmp = s[left];
            s[left] = s[right];
            s[right] = tmp;
        }
    }
}

复杂度分析

  • 时间复杂度：O(N)，其中 N 为字符数组的长度。一共执行了 N/2次的交换。
  • 空间复杂度：O(1)。只使用了常数空间来存放若干变量。

557. 反转字符串中的单词 III

给定一个字符串，你需要反转字符串中每个单词的字符顺序，同时仍保留空格和单词的初始顺序。

示例：

1
2
输入："Let's take LeetCode contest"
输出："s'teL ekat edoCteeL tsetnoc"

方法一：自解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public String reverseWords(String s) {
        String[] s1 = s.split(" ");
        String result = "";
        for (int i = 0; i < s1.length; i++) {
            char[] chars = s1[i].toCharArray();
            String s2 = reverseString1(chars);
            if (i != s1.length-1) {
                result += s2 + " ";
            } else {
                result += s2;
            }
        }
        return result;
    }

    public static String reverseString1(char[] s) {
        int left = 0, right = s.length-1;
        while(left <= right){
            char tmp = s[left];
            s[left] = s[right];
            s[right] = tmp;
            left++;
            right--;
        }
        return String.valueOf(s);
    }
}

方法二：使用额外空间

思路与算法

开辟一个新字符串。然后从头到尾遍历原字符串，直到找到空格为止，此时找到了一个单词，并能得到单词的起止位置。随后，根据单词的起止位置，可以将该单词逆序放到新字符串当中。如此循环多次，直到遍历完原字符串，就能得到翻转后的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public String reverseWords(String s) {
        StringBuffer ret = new StringBuffer();
        int length = s.length();
        int i = 0;
        while (i < length) {
            int start = i;
            // 循环过程中获取逐个单词位置
            while (i < length && s.charAt(i) != ' ') {
                i++;
            }
            for (int p = start; p < i; p++) {
                // 循环去追加倒转后的每个字符
                ret.append(s.charAt(start + i - 1 - p));
            }
            // 每个单词结束追加空格
            while (i < length && s.charAt(i) == ' ') {
                i++;
                ret.append(' ');
            }
        }
        return ret.toString();
    }
}

复杂度分析

  • 时间复杂度：O(N)，其中 N 为字符串的长度。原字符串中的每个字符都会在 O(1) 的时间内放入新字符串中。
  • 空间复杂度：O(N)。我们开辟了与原字符串等大的空间。

方法三：原地解法

思路与算法

此题也可以直接在原字符串上进行操作，避免额外的空间开销。当找到一个单词的时候，我们交换字符串第一个字符与倒数第一个字符，随后交换第二个字符与倒数第二个字符……如此反复，就可以在原空间上翻转单词。

需要注意的是，原地解法在某些语言（比如 Java，JavaScript）中不适用，因为在这些语言中 String 类型是一个不可变的类型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public: 
    string reverseWords(string s) {
        int length = s.length();
        int i = 0;
        while (i < length) {
            int start = i;
            while (i < length && s[i] != ' ') {
                i++;
            }

            int left = start, right = i - 1;
            while (left < right) {
                swap(s[left], s[right]);
                left++;
                right--;
            }
            while (i < length && s[i] == ' ') {
                i++;
            }
        }
        return s;
    }
};

复杂度分析

  • 时间复杂度：O(N)。字符串中的每个字符要么在 O(1) 的时间内被交换到相应的位置，要么因为是空格而保持不动。
  • 空间复杂度：O(1)。因为不需要开辟额外的数组。

876. 链表的中间结点

给定一个头结点为 head 的非空单链表，返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
示例 1：
输入：[1,2,3,4,5]
输出：此列表中的结点 3 (序列化形式：[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意，我们返回了一个 ListNode 类型的对象 ans，这样：
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.

示例 2：
输入：[1,2,3,4,5,6]
输出：此列表中的结点 4 (序列化形式：[4,5,6])
由于该列表有两个中间结点，值分别为 3 和 4，我们返回第二个结点。
 
提示：
给定链表的结点数介于 1 和 100 之间。

方法一：数组

思路和算法

链表的缺点在于不能通过下标访问对应的元素。因此我们可以考虑对链表进行遍历，同时将遍历到的元素依次放入数组 A中。如果我们遍历到了 N 个元素，那么链表以及数组的长度也为 N，对应的中间节点即为 A[N/2]。

1
2
3
4
5
6
7
8
9
10
11
12
public class MiddleNode {
    // 额外的数组空间
    public ListNode middleNode(ListNode head) {
        ListNode[] listNode = new ListNode[100];
        int t = 0;
        while (head != null) {
            listNode[t++] = head;
            head = head.next;
        }
        return listNode[t/2];
    }
}

复杂度分析

  • 时间复杂度：O(N)，其中 N 是给定链表中的结点数目。
  • 空间复杂度：O(N)，即数组 A 用去的空间。

方法二：单指针法

我们可以对方法一进行空间优化，省去数组 A。

我们可以对链表进行两次遍历。第一次遍历时，我们统计链表中的元素个数 N；第二次遍历时，我们遍历到第 N/2 个元素（链表的首节点为第 0 个元素）时，将该元素返回即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class MiddleNode {
    // 单指针
    public ListNode middleNode1(ListNode head) {
        int n = 0;
        ListNode cur = head;
        while (cur != null) {
            ++n;
            cur = cur.next;
        }
        int k = 0;
        cur = head;
        while (k < n / 2) {
            ++k;
            cur = cur.next;
        }
        return cur;
    }
}

复杂度分析

  • 时间复杂度：O(N)，其中 N 是给定链表的结点数目。
  • 空间复杂度：O(1)，只需要常数空间存放变量和指针。

方法三：快慢指针法

思路和算法

我们可以继续优化方法二，用两个指针 slow 与 fast 一起遍历链表。slow 一次走一步，fast 一次走两步。那么当 fast 到达链表的末尾时，slow 必然位于中间。

1
2
3
4
5
6
7
8
9
10
11
public class MiddleNode {
    // 双指针（快慢指针）
    public ListNode middleNode2(ListNode head) {
        ListNode fast = head, slow = head;
        while(fast != null && fast.next != null){
            fast = fast.next.next;
            slow = slow.next;
        }
        return slow;
    }
}

复杂度分析

  • 时间复杂度：O(N)，其中 N 是给定链表的结点数目。
  • 空间复杂度：O(1)，只需要常数空间存放 slow 和 fast 两个指针。

19. 删除链表的倒数第 N 个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

进阶：你能尝试使用一趟扫描实现吗？

示例 1：

image-20210725161622707

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1
输出：[]

示例 3：

输入：head = [1,2], n = 1
输出：[1]

提示：

  • 链表中结点的数目为 sz
  • 1 <= sz <= 30
  • 0 <= Node.val <= 100
  • 1 <= n <= sz

前言
在对链表进行操作时，一种常用的技巧是添加一个哑节点（dummy node），它的next 指针指向链表的头节点。这样一来，我们就不需要对头节点进行特殊的判断了。

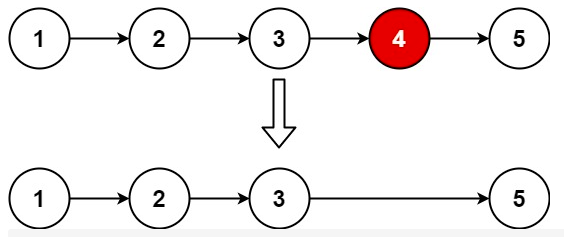
例如，在本题中，如果我们要删除节点 y，我们需要知道节点 y 的前驱节点 x，并将 x 的指针指向 y 的后继节点。但由于头节点不存在前驱节点，因此我们需要在删除头节点时进行特殊判断。但如果我们添加了哑节点，那么头节点的前驱节点就是哑节点本身，此时我们就只需要考虑通用的情况即可。

特别地，在某些语言中，由于需要自行对内存进行管理。因此在实际的面试中，对于「是否需要释放被删除节点对应的空间」这一问题，我们需要和面试官进行积极的沟通以达成一致。下面的代码中默认不释放空间。

方法一：计算链表长度

思路与算法

一种容易想到的方法是，我们首先从头节点开始对链表进行一次遍历，得到链表的长度 L。随后我们再从头节点开始对链表进行一次遍历，当遍历到第L−n+1 个节点时，它就是我们需要删除的节点。

为了与题目中的 n 保持一致，节点的编号从 1 开始，头节点为编号 1 的节点。

为了方便删除操作，我们可以从哑节点开始遍历 L-n+1 个节点。当遍历到第 L-n+1 个节点时，它的下一个节点就是我们需要删除的节点，这样我们只需要修改一次指针，就能完成删除操作。

image-20210725162637102

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(0, head);
        int length = getLength(head);
        // 将创建dummy节点增加在原链表的首节点，这样在处理节点时，不用单独考虑首节点问题
        ListNode cur = dummy;
        for (int i = 1; i < length - n + 1; ++i) {
            cur = cur.next;
        }
        cur.next = cur.next.next;
        ListNode ans = dummy.next;
        return ans;
    }

    // 获取链表的总长度
    public int getLength(ListNode head) {
        int length = 0;
        while (head != null) {
            ++length;
            head = head.next;
        }
        return length;
    }
}

复杂度分析

  • 时间复杂度：O(L)，其中 L 是链表的长度。
  • 空间复杂度：O(1)。

方法二：栈

思路与算法

我们也可以在遍历链表的同时将所有节点依次入栈。根据栈「先进后出」的原则，我们弹出栈的第 n 个节点就是需要删除的节点，并且目前栈顶的节点就是待删除节点的前驱节点。这样一来，删除操作就变得十分方便了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    // 利用栈的先进后出解决问题
    public ListNode removeNthFromEnd2(ListNode head, int n) {
        ListNode dummy = new ListNode(0, head);
        // 利用栈的先进后出解决该问题
        Deque<ListNode> stack = new LinkedList<ListNode>();
        ListNode cur = dummy;
        // 将队列中的所有元素放入栈中（倒序放入）
        while (cur != null) {
            stack.push(cur);
            cur = cur.next;
        }
        // 正序取出 把n前面的所有元素都取出
        for (int i = 0; i < n; ++i) {
            stack.pop();
        }
        //
        ListNode prev = stack.peek();
        // 移除目标元素
        prev.next = prev.next.next;
        ListNode ans = dummy.next;
        return ans;
    }
}

复杂度分析

  • 时间复杂度：O(L)，其中 L 是链表的长度。
  • 空间复杂度：O(L)，其中 L 是链表的长度。主要为栈的开销。

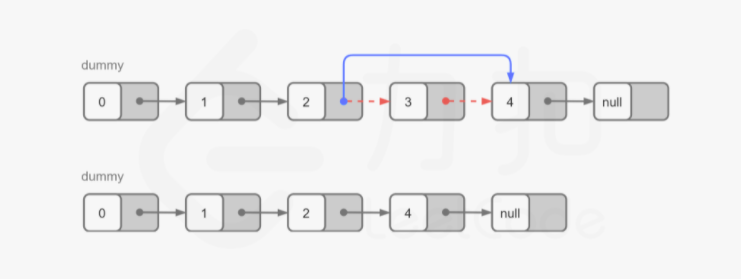
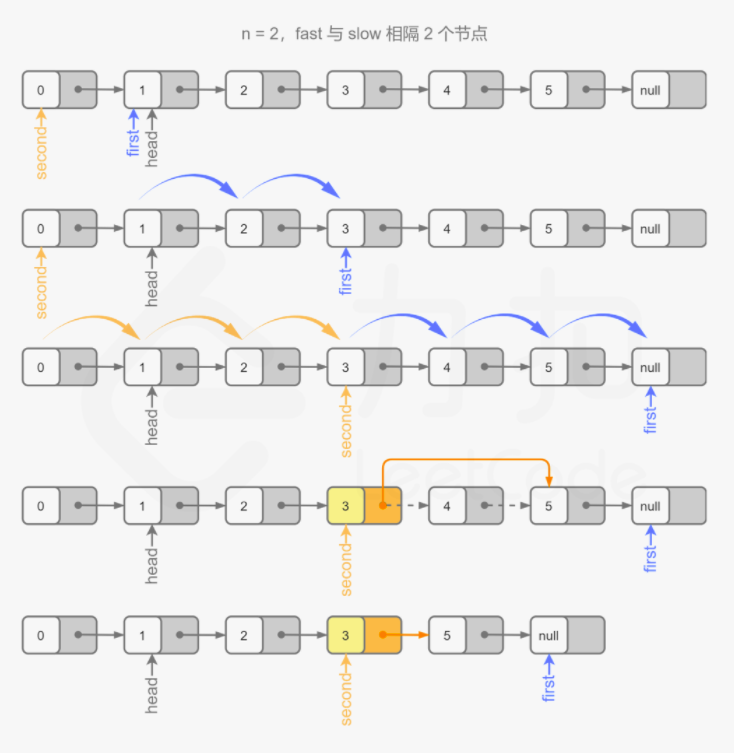
方法三：双指针

思路与算法

我们也可以在不预处理出链表的长度，以及使用常数空间的前提下解决本题。

由于我们需要找到倒数第 n 个节点，因此我们可以使用两个指针 first 和second 同时对链表进行遍历，并且 first 比 second 超前 n 个节点。当 first 遍历到链表的末尾时，second 就恰好处于倒数第 n 个节点。

具体地，初始时 first 和 second 均指向头节点。我们首先使用 first 对链表进行遍历，遍历的次数为 n。此时，first 和 second 之间间隔了 n-1 个节点，即 first 比 second 超前了 n 个节点。

在这之后，我们同时使用 first 和 second 对链表进行遍历。当 first 遍历到链表的末尾（即 first 为空指针）时，second 恰好指向倒数第 n 个节点。

根据方法一和方法二，如果我们能够得到的是倒数第 n 个节点的前驱节点而不是倒数第 n 个节点的话，删除操作会更加方便。因此我们可以考虑在初始时将 second 指向哑节点，其余的操作步骤不变。这样一来，当 first 遍历到链表的末尾时，second 的下一个节点就是我们需要删除的节点。

image-20210725175619995

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    // 快慢指针解决此问题
    public ListNode removeNthFromEnd3(ListNode head, int n) {
        ListNode dummy = new ListNode(0, head);
        ListNode first = head;
        ListNode second = dummy;
        // first默认指向第n-1个元素
        for (int i = 0; i < n; ++i) {
            first = first.next;
        }
        // 遍历至first到达最后一个元素
        while (first != null) {
            first = first.next;
            second = second.next;
        }
        // 移除元素
        second.next = second.next.next;
        ListNode ans = dummy.next;
        return ans;
    }
}

复杂度分析

  • 时间复杂度：O(L)，其中 L 是链表的长度。
  • 空间复杂度：O(1)。

Copyright 2021 sunfy.top ALL Rights Reserved

...

...

00:00
00:00
FEATURED TAGS
FRIENDS