什么是深度优先搜索(DFS)和广度优先搜索(BFS) 图的搜索有两种方式,一种是深度优先搜索(Depth-First-Search),另一种是广度优先搜索(Breadth-First-Search)。
深度优先搜索(DFS)
广度优先搜索(BFS)
深度优先搜索 主要思路是从图中一个未访问的顶点 V 开始,沿着一条路一直走到底,然后从这条路尽头的节点回退到上一个节点,再从另一条路开始走到底…,不断递归重复此过程,直到所有的顶点都遍历完成,它的特点是不撞南墙不回头,先走完一条路,再换一条路继续走。
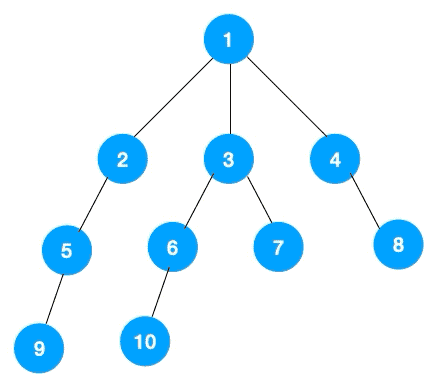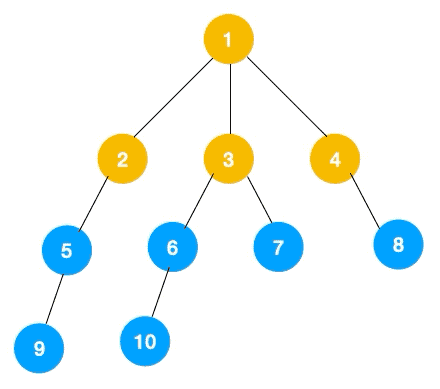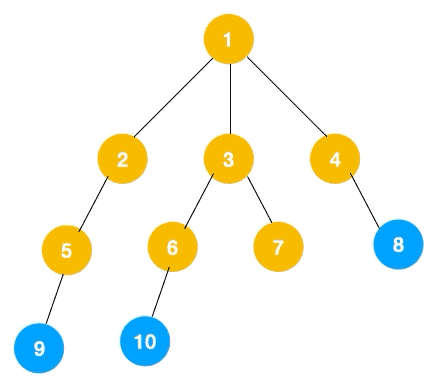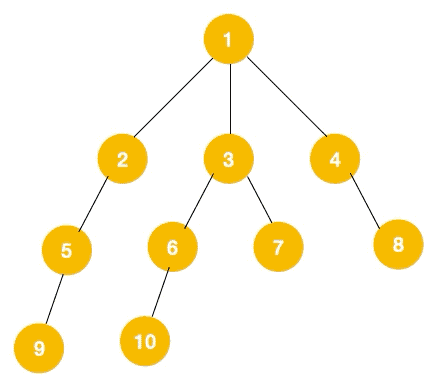
树是图的一种特例(连通无环的图就是树) ,这就是树的前序遍历,实际上不管是前序遍历,还是中序遍历,亦或是后序遍历,都属于深度优先遍历。
遍历二叉树的过程中,一般先遍历左子树,再遍历右子树。在先左后右的原则下,二叉树的遍历分三种
前序遍历:根节点+左子树+右子树。在遍历左子树和右子树时,仍然先访问根节点,然后遍历左子树,最后遍历右子树。
中序遍历:左子树+根节点+右子树。在遍历左右子树时,仍然先遍历左子树,再遍历根节点,后遍历右子树。
后序遍历:左子树+右子树+根节点。在遍历左右子树时,仍然先遍历左子树,在遍历右子树,后访问根节点。
递归实现 递归实现比较简单,由于是前序遍历,所以我们依次遍历当前节点,左节点,右节点即可,对于左右节点来说,依次遍历它们的左右节点即可,依此不断递归下去,直到叶节点(递归终止条件),代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public class Solution private static class Node public int value; public Node left; public Node right; public Node (int value, Node left, Node right) this .value = value; this .left = left; this .right = right; } } public static void dfs (Node treeNode) if (treeNode == null ) { return ; } process(treeNode) dfs(treeNode.left); dfs(treeNode.right); } }
递归的表达性很好,也很容易理解,不过如果层级过深,很容易导致栈溢出。所以我们重点看下非递归实现。
非递归实现 仔细观察深度优先遍历的特点,对二叉树来说,由于是先序遍历(先遍历当前节点,再遍历左节点,再遍历右节点),所以我们有如下思路:
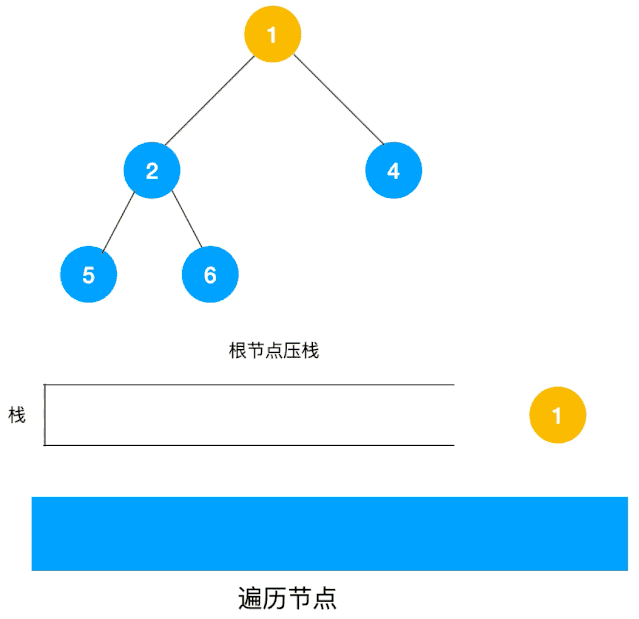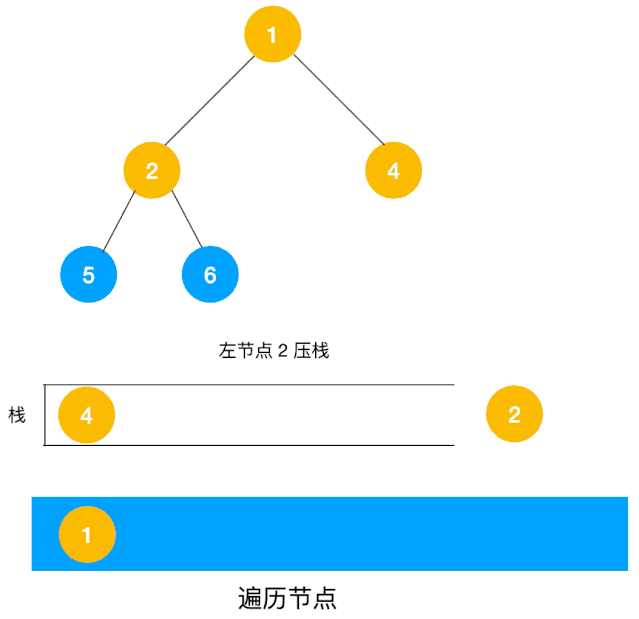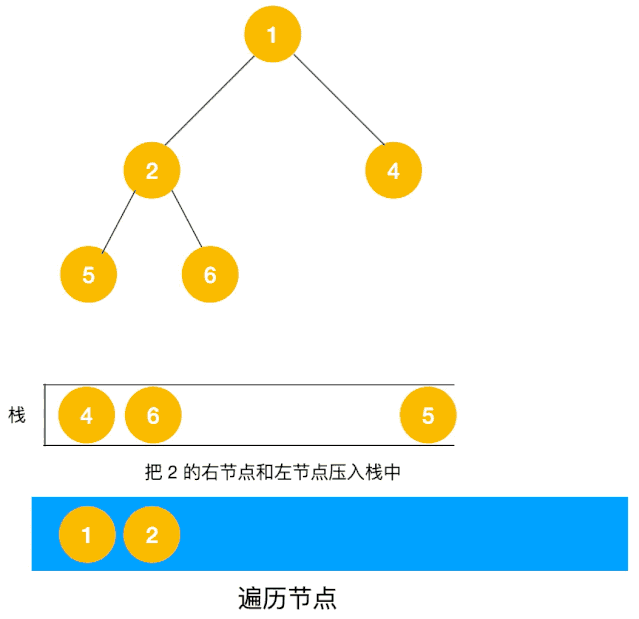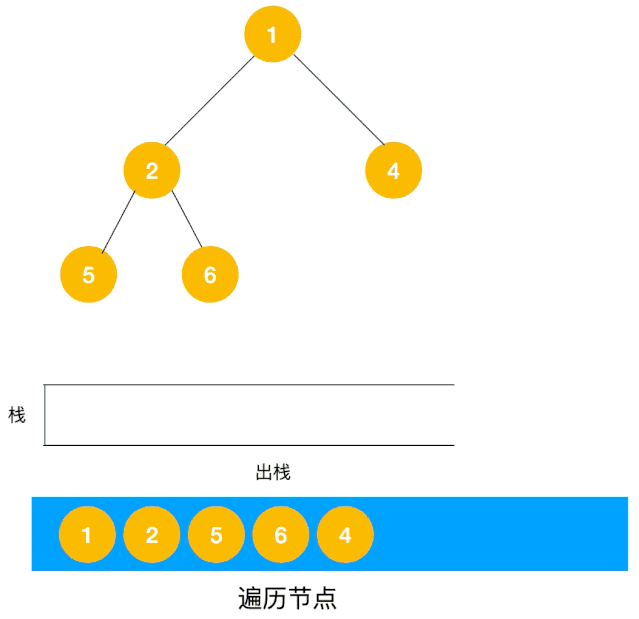
对于每个节点来说,先遍历当前节点,然后把右节点压栈,再压左节点(这样弹栈的时候会先拿到左节点遍历,符合深度优先遍历要求)。
弹栈,拿到栈顶的节点,如果节点不为空,重复步骤 1, 如果为空,结束遍历。
我们以以下二叉树为例来看下如何用栈来实现 DFS。
整体思路还是比较清晰的,使用栈来将要遍历的节点压栈,然后出栈后检查此节点是否还有未遍历的节点,有的话压栈,没有的话不断回溯(出栈),有了思路,不难写出如下用栈实现的二叉树的深度优先遍历代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public static void dfsWithStack (Node root) if (root == null ) { return ; } Stack<Node> stack = new Stack<>(); stack.push(root); while (!stack.isEmpty()) { Node treeNode = stack.pop(); process(treeNode) if (treeNode.right != null ) { stack.push(treeNode.right); } if (treeNode.left != null ) { stack.push(treeNode.left); } } }
可以看到用栈实现深度优先遍历其实代码也不复杂,而且也不用担心递归那样层级过深导致的栈溢出问题。
广度优先搜索 广度优先遍历,指的是从图的一个未遍历的节点出发,先遍历这个节点的相邻节点,再依次遍历每个相邻节点的相邻节点。
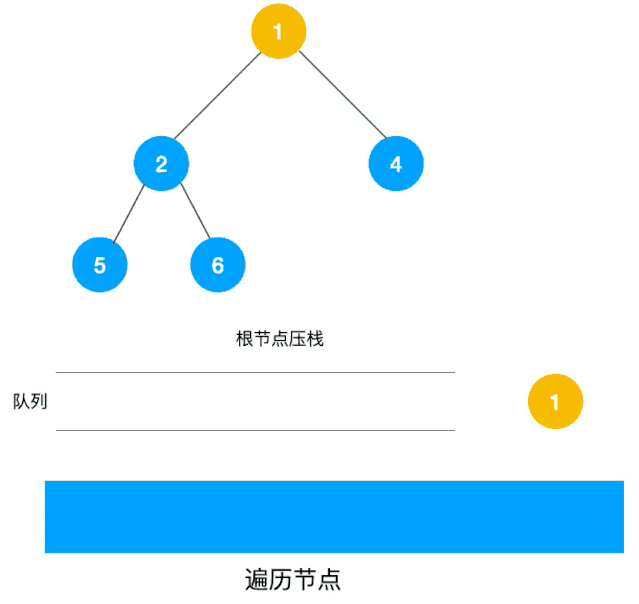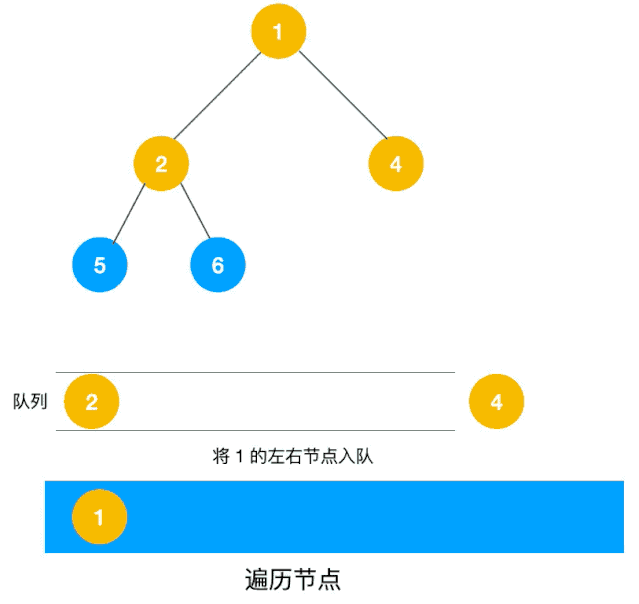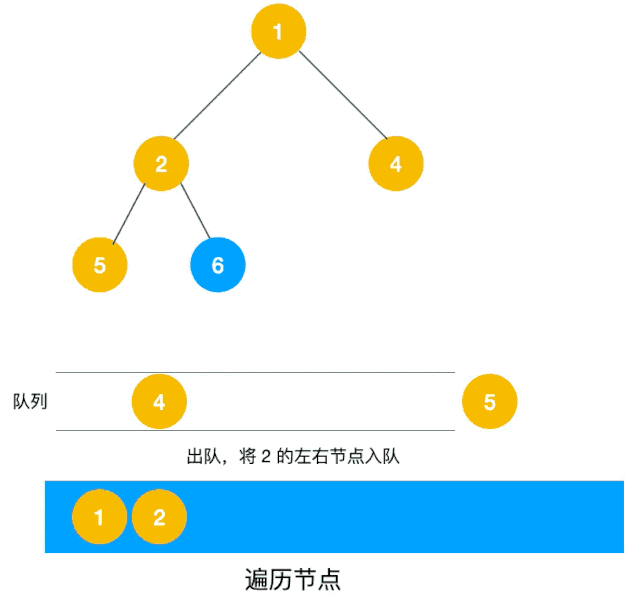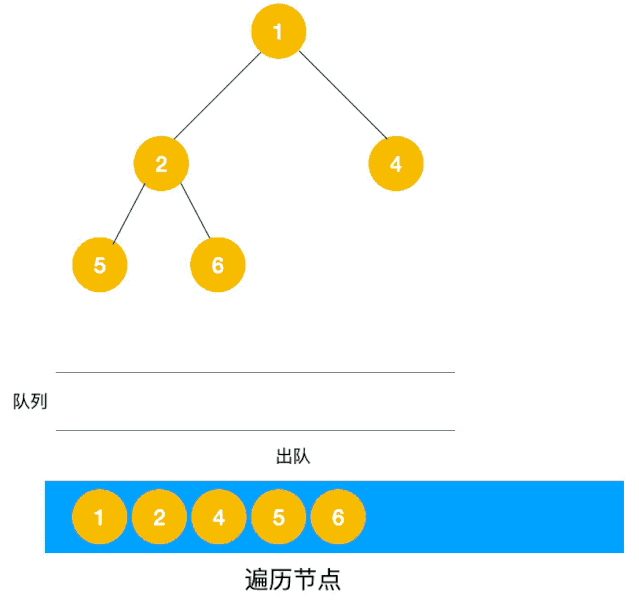
上文所述树的广度优先遍历动图如下,每个节点的值即为它们的遍历顺序。所以广度优先遍历也叫层序遍历,先遍历第一层(节点 1),再遍历第二层(节点 2,3,4),第三层(5,6,7,8),第四层(9,10)。
深度优先遍历用的是栈,而广度优先遍历要用队列来实现,我们以下图二叉树为例来看看如何用队列来实现广度优先遍历。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 private static void bfs (Node root) if (root == null ) { return ; } Queue<Node> stack = new LinkedList<>(); stack.add(root); while (!stack.isEmpty()) { Node node = stack.poll(); System.out.println("value = " + node.value); Node left = node.left; if (left != null ) { stack.add(left); } Node right = node.right; if (right != null ) { stack.add(right); } } }
应用 DFS,BFS 在搜索引擎中的应用我们几乎每天都在 Google, Baidu 这些搜索引擎,那大家知道这些搜索引擎是怎么工作的吗,简单来说有三步:
网页抓取 搜索引擎通过爬虫将网页爬取,获得页面 HTML 代码存入数据库中
预处理 索引程序对抓取来的页面数据进行文字提取,中文分词,(倒排)索引等处理,以备排名程序使用
排名 用户输入关键词后,排名程序调用索引数据库数据,计算相关性,然后按一定格式生成搜索结果页面。
我们重点看下第一步,网页抓取。
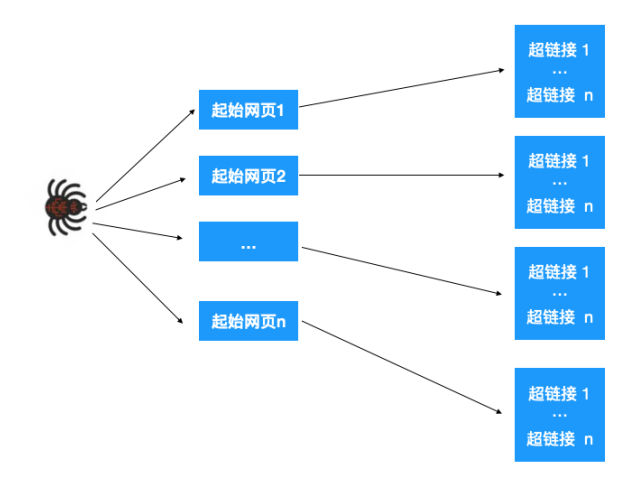
这一步的大致操作如下:给爬虫分配一组起始的网页,我们知道网页里其实也包含了很多超链接,爬虫爬取一个网页后,解析提取出这个网页里的所有超链接,再依次爬取出这些超链接,再提取网页超链接。。。,如此不断重复就能不断根据超链接提取网页。如下图示:
如上所示,最终构成了一张图,于是问题就转化为了如何遍历这张图,显然可以用深度优先或广度优先的方式来遍历。
如果是广度优先遍历,先依次爬取第一层的起始网页,再依次爬取每个网页里的超链接,如果是深度优先遍历,先爬取起始网页 1,再爬取此网页里的链接…,爬取完之后,再爬取起始网页 2…
实际上爬虫是深度优先与广度优先两种策略一起用的,比如在起始网页里,有些网页比较重要(权重较高),那就先对这个网页做深度优先遍历,遍历完之后再对其他(权重一样的)起始网页做广度优先遍历。
总结 DFS 和 BFS 是非常重要的两种算法,大家一定要掌握,本文为了方便讲解,只对树做了 DFS,BFS,大家可以试试如果用图的话该怎么写代码,原理其实也是一样,只不过图和树两者的表示形式不同而已,DFS 一般是解决连通性问题,而 BFS 一般是解决最短路径问题!
有一幅以二维整数数组表示的图画,每一个整数表示该图画的像素值大小,数值在 0 到 65535 之间。
给你一个坐标 (sr, sc) 表示图像渲染开始的像素值(行 ,列)和一个新的颜色值 newColor,让你重新上色这幅图像。
为了完成上色工作,从初始坐标开始,记录初始坐标的上下左右四个方向上像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应四个方向上像素值与初始坐标相同的相连像素点,……,重复该过程。将所有有记录的像素点的颜色值改为新的颜色值。
最后返回经过上色渲染后的图像。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 示例 1: 输入: image = [[1 ,1 ,1 ],[1 ,1 ,0 ],[1 ,0 ,1 ]]sr = 1 , sc = 1 , newColor = 2 输出: [[2,2,2],[2,2,0],[2,0,1]] 解析: 在图像的正中间,(坐标(sr,sc)=(1,1)), 在路径上所有符合条件的像素点的颜色都被更改成2。 注意,右下角的像素没有更改为2, 因为它不是在上下左右四个方向上与初始点相连的像素点。 提示: 1 <= nums.length <= 104 -104 <= nums[i] <= 104 nums 已按 非递减顺序 排序
image 和 image[0] 的长度在范围 [1, 50] 内。给出的初始点将满足 0 <= sr < image.length 和 0 <= sc < image[0].length。
image[i][j] 和 newColor 表示的颜色值在范围 [0, 65535]内。
前言 本题要求将给定的二维数组中指定的「色块」染成另一种颜色。「色块」的定义是:直接或间接相邻的同色方格构成的整体。
可以发现,「色块」就是被不同颜色的方格包围的一个同色岛屿。我们从色块中任意一个地方开始,利用广度优先搜索或深度优先搜索即可遍历整个岛屿。
注意:当目标颜色和初始颜色相同时,我们无需对原数组进行修改。
方法一:广度优先搜索 思路及算法
我们从给定的起点开始,进行广度优先搜索。每次搜索到一个方格时,如果其与初始位置的方格颜色相同,就将该方格加入队列,并将该方格的颜色更新,以防止重复入队。
注意:因为初始位置的颜色会被修改,所以我们需要保存初始位置的颜色,以便于之后的更新操作。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution int [] dx = {1 , 0 , 0 , -1 }; int [] dy = {0 , 1 , -1 , 0 }; public int [][] floodFill(int [][] image, int sr, int sc, int newColor) { int currColor = image[sr][sc]; if (currColor == newColor) { return image; } int n = image.length, m = image[0 ].length; Queue<int []> queue = new LinkedList<int []>(); queue.offer(new int []{sr, sc}); image[sr][sc] = newColor; while (!queue.isEmpty()) { int [] cell = queue.poll(); int x = cell[0 ], y = cell[1 ]; for (int i = 0 ; i < 4 ; i++) { int mx = x + dx[i], my = y + dy[i]; if (mx >= 0 && mx < n && my >= 0 && my < m && image[mx][my] == currColor) { queue.offer(new int []{mx, my}); image[mx][my] = newColor; } } } return image; } }
复杂度分析
时间复杂度:O(n×m),其中 n 和 m 分别是二维数组的行数和列数。最坏情况下需要遍历所有的方格一次。
空间复杂度:O(n×m),其中 n 和 m 分别是二维数组的行数和列数。主要为队列的开销。
方法二:深度优先搜索 思路与算法
我们从给定的起点开始,进行深度优先搜索。每次搜索到一个方格时,如果其与初始位置的方格颜色相同,就将该方格的颜色更新,以防止重复搜索;如果不相同,则进行回溯。
注意:因为初始位置的颜色会被修改,所以我们需要保存初始位置的颜色,以便于之后的更新操作。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution int [] dx = {1 , 0 , 0 , -1 }; int [] dy = {0 , 1 , -1 , 0 }; public int [][] floodFill(int [][] image, int sr, int sc, int newColor) { int currColor = image[sr][sc]; if (currColor != newColor) { dfs(image, sr, sc, currColor, newColor); } return image; } public void dfs (int [][] image, int x, int y, int color, int newColor) if (image[x][y] == color) { image[x][y] = newColor; for (int i = 0 ; i < 4 ; i++) { int mx = x + dx[i], my = y + dy[i]; if (mx >= 0 && mx < image.length && my >= 0 && my < image[0 ].length) { dfs(image, mx, my, color, newColor); } } } } }
复杂度分析
时间复杂度:O(n×m),其中 n 和 m 分别是二维数组的行数和列数。最坏情况下需要遍历所有的方格一次。
空间复杂度:O(n×m),其中 n 和 m 分别是二维数组的行数和列数。主要为栈空间的开销。
给定一个包含了一些 0 和 1 的非空二维数组 grid。
一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 示例 1: [[0,0,1,0,0,0,0,1,0,0,0,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,1,1,0,1,0,0,0,0,0,0,0,0], [0,1,0,0,1,1,0,0,1,0,1,0,0], [0,1,0,0,1,1,0,0,1,1,1,0,0], [0,0,0,0,0,0,0,0,0,0,1,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,0,0,0,0,0,0,1,1,0,0,0,0]] 对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ,因为岛屿只能包含水平或垂直的四个方向的 1 。 示例 2: [[0,0,0,0,0,0,0,0]] 对于上面这个给定的矩阵, 返回 0。 注意: 给定的矩阵grid 的长度和宽度都不超过 50。
方法一:深度优先搜索 算法
我们想知道网格中每个连通形状的面积,然后取最大值。
如果我们在一个土地上,以 44 个方向探索与之相连的每一个土地(以及与这些土地相连的土地),那么探索过的土地总数将是该连通形状的面积。
为了确保每个土地访问不超过一次,我们每次经过一块土地时,将这块土地的值置为 00。这样我们就不会多次访问同一土地。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution public int maxAreaOfIsland (int [][] grid) int ans = 0 ; for (int i = 0 ; i != grid.length; ++i) { for (int j = 0 ; j != grid[0 ].length; ++j) { ans = Math.max(ans, dfs(grid, i, j)); } } return ans; } public int dfs (int [][] grid, int cur_i, int cur_j) if (cur_i < 0 || cur_j < 0 || cur_i == grid.length || cur_j == grid[0 ].length || grid[cur_i][cur_j] != 1 ) { return 0 ; } grid[cur_i][cur_j] = 0 ; int [] di = {0 , 0 , 1 , -1 }; int [] dj = {1 , -1 , 0 , 0 }; int ans = 1 ; for (int index = 0 ; index != 4 ; ++index) { int next_i = cur_i + di[index], next_j = cur_j + dj[index]; ans += dfs(grid, next_i, next_j); } return ans; } }
复杂度分析
时间复杂度:O(R×C)。其中 R 是给定网格中的行数,C 是列数。我们访问每个网格最多一次。
空间复杂度:O(R×C),递归的深度最大可能是整个网格的大小,因此最大可能使用 O(R×C) 的栈空间。
方法二:深度优先搜索 + 栈 算法
我们可以用栈来实现深度优先搜索算法。这种方法本质与方法一相同,唯一的区别是:
方法一通过函数的调用来表示接下来想要遍历哪些土地,让下一层函数来访问这些土地。而方法二把接下来想要遍历的土地放在栈里,然后在取出这些土地的时候访问它们。
访问每一片土地时,我们将对围绕它四个方向进行探索,找到还未访问的土地,加入到栈 stack 中;
另外,只要栈 stack 不为空,就说明我们还有土地待访问,那么就从栈中取出一个元素并访问。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution public int maxAreaOfIsland (int [][] grid) int ans = 0 ; for (int i = 0 ; i != grid.length; ++i) { for (int j = 0 ; j != grid[0 ].length; ++j) { int cur = 0 ; Deque<Integer> stacki = new LinkedList<Integer>(); Deque<Integer> stackj = new LinkedList<Integer>(); stacki.push(i); stackj.push(j); while (!stacki.isEmpty()) { int cur_i = stacki.pop(), cur_j = stackj.pop(); if (cur_i < 0 || cur_j < 0 || cur_i == grid.length || cur_j == grid[0 ].length || grid[cur_i][cur_j] != 1 ) { continue ; } ++cur; grid[cur_i][cur_j] = 0 ; int [] di = {0 , 0 , 1 , -1 }; int [] dj = {1 , -1 , 0 , 0 }; for (int index = 0 ; index != 4 ; ++index) { int next_i = cur_i + di[index], next_j = cur_j + dj[index]; stacki.push(next_i); stackj.push(next_j); } } ans = Math.max(ans, cur); } } return ans; } }
复杂度分析
时间复杂度:O(R×C)。其中 RR 是给定网格中的行数,C 是列数。我们访问每个网格最多一次。
空间复杂度:O(R×C),栈中最多会存放所有的土地,土地的数量最多为 R×C 块,因此使用的空间为 O(R×C)。
方法三:广度优先搜索 算法
我们把方法二中的栈改为队列,每次从队首取出土地,并将接下来想要遍历的土地放在队尾,就实现了广度优先搜索算法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution public int maxAreaOfIsland (int [][] grid) int ans = 0 ; for (int i = 0 ; i != grid.length; ++i) { for (int j = 0 ; j != grid[0 ].length; ++j) { int cur = 0 ; Queue<Integer> queuei = new LinkedList<Integer>(); Queue<Integer> queuej = new LinkedList<Integer>(); queuei.offer(i); queuej.offer(j); while (!queuei.isEmpty()) { int cur_i = queuei.poll(), cur_j = queuej.poll(); if (cur_i < 0 || cur_j < 0 || cur_i == grid.length || cur_j == grid[0 ].length || grid[cur_i][cur_j] != 1 ) { continue ; } ++cur; grid[cur_i][cur_j] = 0 ; int [] di = {0 , 0 , 1 , -1 }; int [] dj = {1 , -1 , 0 , 0 }; for (int index = 0 ; index != 4 ; ++index) { int next_i = cur_i + di[index], next_j = cur_j + dj[index]; queuei.offer(next_i); queuej.offer(next_j); } } ans = Math.max(ans, cur); } } return ans; } }
复杂度分析
时间复杂度:O(R×C)。其中 R 是给定网格中的行数,C 是列数。我们访问每个网格最多一次。
空间复杂度:O(R×C),队列中最多会存放所有的土地,土地的数量最多为 R×C 块,因此使用的空间为 O(R×C)。
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 示例 1: 输入: Tree 1 Tree 2 1 2 / \ / \ 3 2 1 3 / \ \ 5 4 7 输出: 合并后的树: 3 / \ 4 5 / \ \ 5 4 7 注意: 合并必须从两个树的根节点开始。
方法一:深度优先搜索 可以使用深度优先搜索合并两个二叉树。从根节点开始同时遍历两个二叉树,并将对应的节点进行合并。
两个二叉树的对应节点可能存在以下三种情况,对于每种情况使用不同的合并方式。
如果两个二叉树的对应节点都为空,则合并后的二叉树的对应节点也为空;
如果两个二叉树的对应节点只有一个为空,则合并后的二叉树的对应节点为其中的非空节点;
如果两个二叉树的对应节点都不为空,则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和,此时需要显性合并两个节点。
对一个节点进行合并之后,还要对该节点的左右子树分别进行合并。这是一个递归的过程。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution public TreeNode mergeTrees (TreeNode t1, TreeNode t2) if (t1 == null ) { return t2; } if (t2 == null ) { return t1; } TreeNode merged = new TreeNode(t1.val + t2.val); merged.left = mergeTrees(t1.left, t2.left); merged.right = mergeTrees(t1.right, t2.right); return merged; } }
复杂度分析
时间复杂度:O(min(m,n)),其中 m 和 n 分别是两个二叉树的节点个数。对两个二叉树同时进行深度优先搜索,只有当两个二叉树中的对应节点都不为空时才会对该节点进行显性合并操作,因此被访问到的节点数不会超过较小的二叉树的节点数。
空间复杂度:O(min(m,n)),其中 m 和 n 分别是两个二叉树的节点个数。空间复杂度取决于递归调用的层数,递归调用的层数不会超过较小的二叉树的最大高度,最坏情况下,二叉树的高度等于节点数。
方法二:广度优先搜索 也可以使用广度优先搜索合并两个二叉树。首先判断两个二叉树是否为空,如果两个二叉树都为空,则合并后的二叉树也为空,如果只有一个二叉树为空,则合并后的二叉树为另一个非空的二叉树。
如果两个二叉树都不为空,则首先计算合并后的根节点的值,然后从合并后的二叉树与两个原始二叉树的根节点开始广度优先搜索,从根节点开始同时遍历每个二叉树,并将对应的节点进行合并。
使用三个队列分别存储合并后的二叉树的节点以及两个原始二叉树的节点。初始时将每个二叉树的根节点分别加入相应的队列。每次从每个队列中取出一个节点,判断两个原始二叉树的节点的左右子节点是否为空。如果两个原始二叉树的当前节点中至少有一个节点的左子节点不为空,则合并后的二叉树的对应节点的左子节点也不为空。对于右子节点同理。
如果合并后的二叉树的左子节点不为空,则需要根据两个原始二叉树的左子节点计算合并后的二叉树的左子节点以及整个左子树。考虑以下两种情况:
如果两个原始二叉树的左子节点都不为空,则合并后的二叉树的左子节点的值为两个原始二叉树的左子节点的值之和,在创建合并后的二叉树的左子节点之后,将每个二叉树中的左子节点都加入相应的队列;
如果两个原始二叉树的左子节点有一个为空,即有一个原始二叉树的左子树为空,则合并后的二叉树的左子树即为另一个原始二叉树的左子树,此时也不需要对非空左子树继续遍历,因此不需要将左子节点加入队列。
对于右子节点和右子树,处理方法与左子节点和左子树相同。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 class Solution public TreeNode mergeTrees (TreeNode t1, TreeNode t2) if (t1 == null ) { return t2; } if (t2 == null ) { return t1; } TreeNode merged = new TreeNode(t1.val + t2.val); Queue<TreeNode> queue = new LinkedList<TreeNode>(); Queue<TreeNode> queue1 = new LinkedList<TreeNode>(); Queue<TreeNode> queue2 = new LinkedList<TreeNode>(); queue.offer(merged); queue1.offer(t1); queue2.offer(t2); while (!queue1.isEmpty() && !queue2.isEmpty()) { TreeNode node = queue.poll(), node1 = queue1.poll(), node2 = queue2.poll(); TreeNode left1 = node1.left, left2 = node2.left, right1 = node1.right, right2 = node2.right; if (left1 != null || left2 != null ) { if (left1 != null && left2 != null ) { TreeNode left = new TreeNode(left1.val + left2.val); node.left = left; queue.offer(left); queue1.offer(left1); queue2.offer(left2); } else if (left1 != null ) { node.left = left1; } else if (left2 != null ) { node.left = left2; } } if (right1 != null || right2 != null ) { if (right1 != null && right2 != null ) { TreeNode right = new TreeNode(right1.val + right2.val); node.right = right; queue.offer(right); queue1.offer(right1); queue2.offer(right2); } else if (right1 != null ) { node.right = right1; } else { node.right = right2; } } } return merged; } }
复杂度分析
时间复杂度:O(min(m,n)),其中 m 和 n 分别是两个二叉树的节点个数。对两个二叉树同时进行广度优先搜索,只有当两个二叉树中的对应节点都不为空时才会访问到该节点,因此被访问到的节点数不会超过较小的二叉树的节点数。
空间复杂度:O(min(m,n)),其中 m 和 n 分别是两个二叉树的节点个数。空间复杂度取决于队列中的元素个数,队列中的元素个数不会超过较小的二叉树的节点数。
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
1 2 3 4 5 6 struct Node { int val; Node *left; Node *right; Node *next; }
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
进阶:
你只能使用常量级额外空间。
使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
实例:
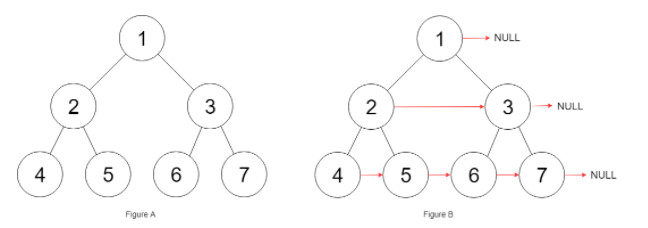
1 2 3 输入:root = [1,2,3,4,5,6,7] 输出:[1,#,2,3,#,4,5,6,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
提示:
树中节点的数量少于 4096
-1000 <= node.val <= 1000
方法一:层次遍历 思路与算法
题目本身希望我们将二叉树的每一层节点都连接起来形成一个链表。因此直观的做法我们可以对二叉树进行层次遍历,在层次遍历的过程中将我们将二叉树每一层的节点拿出来遍历并连接。
层次遍历基于广度优先搜索,它与广度优先搜索的不同之处在于,广度优先搜索每次只会取出一个节点来拓展,而层次遍历会每次将队列中的所有元素都拿出来拓展,这样能保证每次从队列中拿出来遍历的元素都是属于同一层的,因此我们可以在遍历的过程中修改每个节点的 \text{next}next 指针,同时拓展下一层的新队列。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution public Node connect (Node root) if (root == null ) { return root; } Queue<Node> queue = new LinkedList<Node>(); queue.add(root); while (!queue.isEmpty()) { int size = queue.size(); for (int i = 0 ; i < size; i++) { Node node = queue.poll(); if (i < size - 1 ) { node.next = queue.peek(); } if (node.left != null ) { queue.add(node.left); } if (node.right != null ) { queue.add(node.right); } } } return root; } }
复杂度分析
时间复杂度:O(N)。每个节点会被访问一次且只会被访问一次,即从队列中弹出,并建立 next 指针。
空间复杂度:O(N)。这是一棵完美二叉树,它的最后一个层级包含 N/2 个节点。广度优先遍历的复杂度取决于一个层级上的最大元素数量。这种情况下空间复杂度为 O(N)。
方法二:使用已建立的 next 指针 思路
一棵树中,存在两种类型的 next 指针。
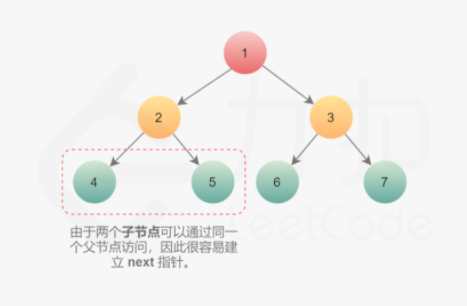
第一种情况是连接同一个父节点的两个子节点。它们可以通过同一个节点直接访问到,因此执行下面操作即可完成连接。
1 node.left.next = node.right
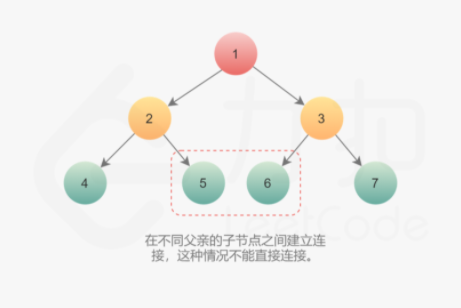
第二种情况在不同父亲的子节点之间建立连接,这种情况不能直接连接。
如果每个节点有指向父节点的指针,可以通过该指针找到 \text{next}next 节点。如果不存在该指针,则按照下面思路建立连接:
第 N 层节点之间建立 next 指针后,再建立第 N+1 层节点的 next 指针。可以通过 next 指针访问同一层的所有节点,因此可以使用第 N 层的 next 指针,为第 N+1 层节点建立 next 指针。
算法
从根节点开始,由于第 0 层只有一个节点,所以不需要连接,直接为第 1 层节点建立next 指针即可。该算法中需要注意的一点是,当我们为第 N 层节点建立 next 指针时,处于第 N-1 层。当第 N 层节点的 next 指针全部建立完成后,移至第 N 层,建立第 N+1 层节点的 next 指针。
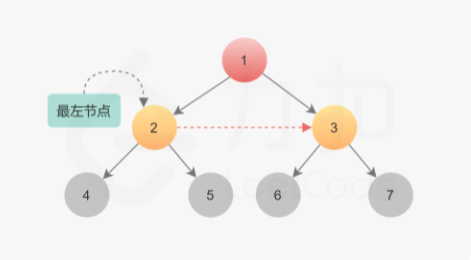
遍历某一层的节点时,这层节点的 next 指针已经建立。因此我们只需要知道这一层的最左节点,就可以按照链表方式遍历,不需要使用队列。
上面思路的伪代码如下:
1 2 3 4 5 6 7 8 9 10 leftmost = rootwhile (leftmost.left != null) { head = leftmost while (head.next != null) { 1) Establish Connection 1 2) Establish Connection 2 using next pointers head = head.next } leftmost = leftmost.left }
两种类型的 next 指针。
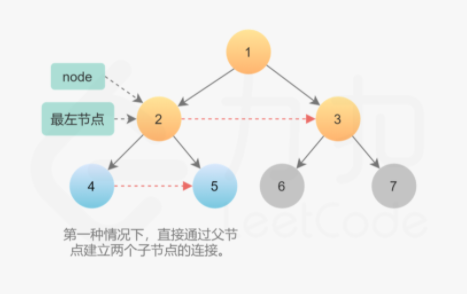
第一种情况两个子节点属于同一个父节点,因此直接通过父节点建立两个子节点的 next 指针即可。
1 node.left.next = node.right
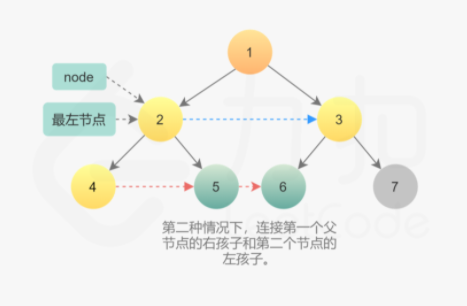
第二种情况是连接不同父节点之间子节点的情况。更具体地说,连接的是第一个父节点的右孩子和第二父节点的左孩子。由于已经在父节点这一层建立了 next 指针,因此可以直接通过第一个父节点的 next 指针找到第二个父节点,然后在它们的孩子之间建立连接。
1 node.right.next = node.next.left
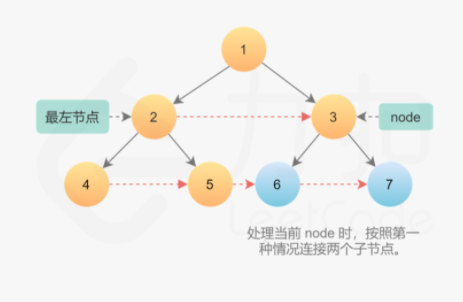
完成当前层的连接后,进入下一层重复操作,直到所有的节点全部连接。进入下一层后需要更新最左节点,然后从新的最左节点开始遍历该层所有节点。因为是完美二叉树,因此最左节点一定是当前层最左节点的左孩子。如果当前最左节点的左孩子不存在,说明已经到达该树的最后一层,完成了所有节点的连接。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution public Node connect (Node root) if (root == null ) { return root; } Node leftmost = root; while (leftmost.left != null ) { Node head = leftmost; while (head != null ) { head.left.next = head.right; if (head.next != null ) { head.right.next = head.next.left; } head = head.next; } leftmost = leftmost.left; } return root; } }
复杂度分析
时间复杂度:O(N),每个节点只访问一次。
空间复杂度:O(1),不需要存储额外的节点。
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
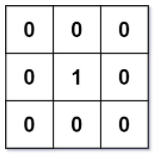
1 2 输入:mat = [[0,0,0],[0,1,0],[0,0,0]] 输出:[[0,0,0],[0,1,0],[0,0,0]]
示例 2:
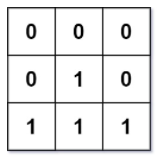
1 2 输入:mat = [[0,0,0],[0,1,0],[1,1,1]] 输出:[[0,0,0],[0,1,0],[1,2,1]]
提示:
m == mat.length
n == mat[i].length
1 <= m, n <= 104
1 <= m * n <= 104
mat[i][j] is either 0 or 1.
mat 中至少有一个 0
方法一:广度优先搜索
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution static int [][] dirs = {{-1 , 0 }, {1 , 0 }, {0 , -1 }, {0 , 1 }}; public int [][] updateMatrix(int [][] matrix) { int m = matrix.length, n = matrix[0 ].length; int [][] dist = new int [m][n]; boolean [][] seen = new boolean [m][n]; Queue<int []> queue = new LinkedList<int []>(); for (int i = 0 ; i < m; ++i) { for (int j = 0 ; j < n; ++j) { if (matrix[i][j] == 0 ) { queue.offer(new int []{i, j}); seen[i][j] = true ; } } } while (!queue.isEmpty()) { int [] cell = queue.poll(); int i = cell[0 ], j = cell[1 ]; for (int d = 0 ; d < 4 ; ++d) { int ni = i + dirs[d][0 ]; int nj = j + dirs[d][1 ]; if (ni >= 0 && ni < m && nj >= 0 && nj < n && !seen[ni][nj]) { dist[ni][nj] = dist[i][j] + 1 ; queue.offer(new int []{ni, nj}); seen[ni][nj] = true ; } } } return dist; } }
方法二:动态规划
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 class Solution static int [][] dirs = {{-1 , 0 }, {1 , 0 }, {0 , -1 }, {0 , 1 }}; public int [][] updateMatrix(int [][] matrix) { int m = matrix.length, n = matrix[0 ].length; int [][] dist = new int [m][n]; for (int i = 0 ; i < m; ++i) { Arrays.fill(dist[i], Integer.MAX_VALUE / 2 ); } for (int i = 0 ; i < m; ++i) { for (int j = 0 ; j < n; ++j) { if (matrix[i][j] == 0 ) { dist[i][j] = 0 ; } } } for (int i = 0 ; i < m; ++i) { for (int j = 0 ; j < n; ++j) { if (i - 1 >= 0 ) { dist[i][j] = Math.min(dist[i][j], dist[i - 1 ][j] + 1 ); } if (j - 1 >= 0 ) { dist[i][j] = Math.min(dist[i][j], dist[i][j - 1 ] + 1 ); } } } for (int i = m - 1 ; i >= 0 ; --i) { for (int j = 0 ; j < n; ++j) { if (i + 1 < m) { dist[i][j] = Math.min(dist[i][j], dist[i + 1 ][j] + 1 ); } if (j - 1 >= 0 ) { dist[i][j] = Math.min(dist[i][j], dist[i][j - 1 ] + 1 ); } } } for (int i = 0 ; i < m; ++i) { for (int j = n - 1 ; j >= 0 ; --j) { if (i - 1 >= 0 ) { dist[i][j] = Math.min(dist[i][j], dist[i - 1 ][j] + 1 ); } if (j + 1 < n) { dist[i][j] = Math.min(dist[i][j], dist[i][j + 1 ] + 1 ); } } } for (int i = m - 1 ; i >= 0 ; --i) { for (int j = n - 1 ; j >= 0 ; --j) { if (i + 1 < m) { dist[i][j] = Math.min(dist[i][j], dist[i + 1 ][j] + 1 ); } if (j + 1 < n) { dist[i][j] = Math.min(dist[i][j], dist[i][j + 1 ] + 1 ); } } } return dist; } }
方法三:动态规划的常数优化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Solution static int [][] dirs = {{-1 , 0 }, {1 , 0 }, {0 , -1 }, {0 , 1 }}; public int [][] updateMatrix(int [][] matrix) { int m = matrix.length, n = matrix[0 ].length; int [][] dist = new int [m][n]; for (int i = 0 ; i < m; ++i) { Arrays.fill(dist[i], Integer.MAX_VALUE / 2 ); } for (int i = 0 ; i < m; ++i) { for (int j = 0 ; j < n; ++j) { if (matrix[i][j] == 0 ) { dist[i][j] = 0 ; } } } for (int i = 0 ; i < m; ++i) { for (int j = 0 ; j < n; ++j) { if (i - 1 >= 0 ) { dist[i][j] = Math.min(dist[i][j], dist[i - 1 ][j] + 1 ); } if (j - 1 >= 0 ) { dist[i][j] = Math.min(dist[i][j], dist[i][j - 1 ] + 1 ); } } } for (int i = m - 1 ; i >= 0 ; --i) { for (int j = n - 1 ; j >= 0 ; --j) { if (i + 1 < m) { dist[i][j] = Math.min(dist[i][j], dist[i + 1 ][j] + 1 ); } if (j + 1 < n) { dist[i][j] = Math.min(dist[i][j], dist[i][j + 1 ] + 1 ); } } } return dist; } }
在给定的网格中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1。
实例1:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 输入:[[2,1,1],[1,1,0],[0,1,1]] 输出:4 示例 2: 输入:[[2,1,1],[0,1,1],[1,0,1]] 输出:-1 解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个正向上。 示例 3: 输入:[[0,2]] 输出:0 解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。 提示: 1 <= grid.length <= 10 1 <= grid[0].length <= 10 grid[i][j] 仅为 0、1 或 2
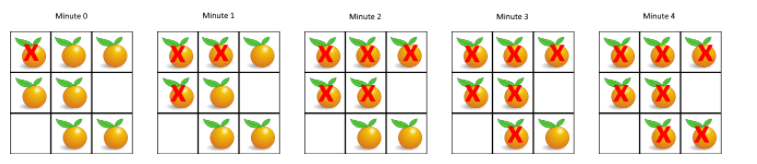
前言 由题目我们可以知道每分钟每个腐烂的橘子都会使上下左右相邻的新鲜橘子腐烂,这其实是一个模拟广度优先搜索的过程。所谓广度优先搜索,就是从起点出发,每次都尝试访问同一层的节点,如果同一层都访问完了,再访问下一层,最后广度优先搜索找到的路径就是从起点开始的最短合法路径。
回到题目中,假设图中只有一个腐烂的橘子,它每分钟向外拓展,腐烂上下左右相邻的新鲜橘子,那么下一分钟,就是这些被腐烂的橘子再向外拓展腐烂相邻的新鲜橘子,这与广度优先搜索的过程均一一对应,上下左右相邻的新鲜橘子就是该腐烂橘子尝试访问的同一层的节点,路径长度就是新鲜橘子被腐烂的时间。我们记录下每个新鲜橘子被腐烂的时间,最后如果单元格中没有新鲜橘子,腐烂所有新鲜橘子所必须经过的最小分钟数就是新鲜橘子被腐烂的时间的最大值。
以上是基于图中只有一个腐烂的橘子的情况,可实际题目中腐烂的橘子数不止一个,看似与广度优先搜索有所区别,不能直接套用,但其实有两个方向的思路。
一个是耗时比较大且不推荐的做法:我们对每个腐烂橘子为起点都进行一次广度优先搜索,用
最后的答案就是所有新鲜橘子被腐烂的最短时间的最大值,如果是无限大,说明有新鲜橘子没有被腐烂,输出 -1 即可。
无疑上面的方法需要枚举每个腐烂橘子,所以时间复杂度需要在原先广度优先搜索遍历的时间复杂度上再乘以腐烂橘子数,这在整个网格范围变大的时候十分耗时,所以需要另寻他路。
方法一:多源广度优先搜索 思路
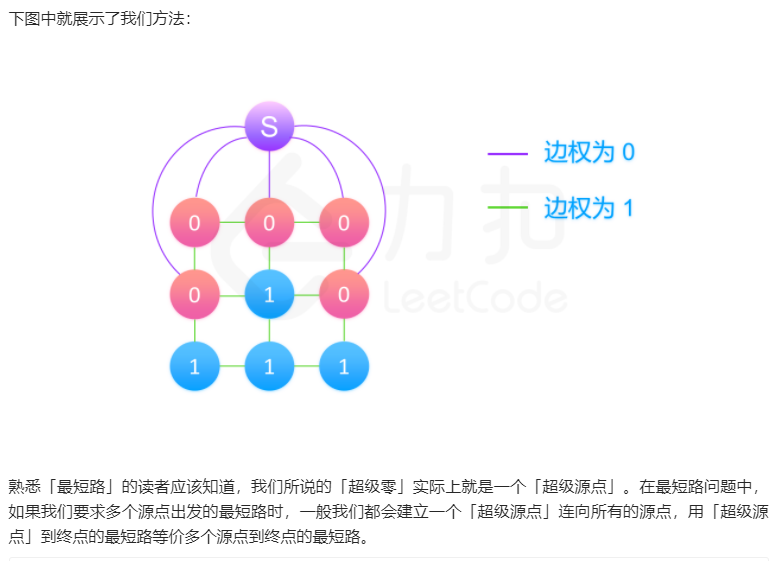
观察到对于所有的腐烂橘子,其实它们在广度优先搜索上是等价于同一层的节点的。
假设这些腐烂橘子刚开始是新鲜的,而有一个腐烂橘子(我们令其为超级源点)会在下一秒把这些橘子都变腐烂,而这个腐烂橘子刚开始在的时间是 −1 ,那么按照广度优先搜索的算法,下一分钟也就是第 0 分钟的时候,这个腐烂橘子会把它们都变成腐烂橘子,然后继续向外拓展,所以其实这些腐烂橘子是同一层的节点。那么在广度优先搜索的时候,我们将这些腐烂橘子都放进队列里进行广度优先搜索即可,最后每个新鲜橘子被腐烂的最短时间 dis[x][y] 其实是以这个超级源点的腐烂橘子为起点的广度优先搜索得到的结果。
为了确认是否所有新鲜橘子都被腐烂,可以记录一个变量 cnt 表示当前网格中的新鲜橘子数,广度优先搜索的时候如果有新鲜橘子被腐烂,则 cnt-=1 ,最后搜索结束时如果cnt 大于 0 ,说明有新鲜橘子没被腐烂,返回 -1 ,否则返回所有新鲜橘子被腐烂的时间的最大值即可,也可以在广度优先搜索的过程中把已腐烂的新鲜橘子的值由 1 改为 2,最后看网格中是否由值为 1 即新鲜的橘子即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Solution int [] dr = new int []{-1 , 0 , 1 , 0 }; int [] dc = new int []{0 , -1 , 0 , 1 }; public int orangesRotting (int [][] grid) int R = grid.length, C = grid[0 ].length; Queue<Integer> queue = new ArrayDeque<Integer>(); Map<Integer, Integer> depth = new HashMap<Integer, Integer>(); for (int r = 0 ; r < R; ++r) { for (int c = 0 ; c < C; ++c) { if (grid[r][c] == 2 ) { int code = r * C + c; queue.add(code); depth.put(code, 0 ); } } } int ans = 0 ; while (!queue.isEmpty()) { int code = queue.remove(); int r = code / C, c = code % C; for (int k = 0 ; k < 4 ; ++k) { int nr = r + dr[k]; int nc = c + dc[k]; if (0 <= nr && nr < R && 0 <= nc && nc < C && grid[nr][nc] == 1 ) { grid[nr][nc] = 2 ; int ncode = nr * C + nc; queue.add(ncode); depth.put(ncode, depth.get(code) + 1 ); ans = depth.get(ncode); } } } for (int [] row: grid) { for (int v: row) { if (v == 1 ) { return -1 ; } } } return ans; } }
复杂度分析
时间复杂度:O(nm)n=grid.length, m=grid[0].length 。
空间复杂度:O(nm)dis 数组记录每个新鲜橘子被腐烂的最短时间,大小为 O(nm),且广度优先搜索中队列里存放的状态最多不会超过 nm 个,最多需要O(nm) 的空间,所以最后的空间复杂度为 O(nm)。











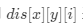 表示只考虑第 ii 个腐烂橘子为起点的广度优先搜索,坐标位于 (x, y)(x,y) 的新鲜橘子被腐烂的时间,设没有被腐烂的新鲜橘子的
表示只考虑第 ii 个腐烂橘子为起点的广度优先搜索,坐标位于 (x, y)(x,y) 的新鲜橘子被腐烂的时间,设没有被腐烂的新鲜橘子的 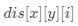 ,即无限大,表示没有被腐烂,那么每个新鲜橘子被腐烂的最短时间即为
,即无限大,表示没有被腐烂,那么每个新鲜橘子被腐烂的最短时间即为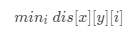
Copyright 2021 sunfy.top ALL Rights Reserved