动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的过程。20世纪50年代初,美国数学家贝尔曼(R.Bellman)等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,从而创立了动态规划。动态规划的应用极其广泛,包括工程技术、经济、工业生产、军事以及自动化控制等领域,并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果 [1] 。 [2]
基本概念
基本结构
多阶段决策问题中,各个阶段采取的决策,一般来说是与时间有关的,决策依赖于当前状态,又随即引起状态的转移,一个决策序列就是在变化的状态中产生出来的,故有“动态”的含义,称这种解决多阶段决策最优化问题的方法为动态规划方法 [7] 。
适用条件
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| 示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
|
方法一:动态规划
思路和算法
我们用 f(x) 表示爬到第 xx 级台阶的方案数,考虑最后一步可能跨了一级台阶,也可能跨了两级台阶,所以我们可以列出如下式子:
f(x) = f(x - 1) + f(x - 2)
它意味着爬到第 x 级台阶的方案数是爬到第 x - 1 级台阶的方案数和爬到第 x - 2 级台阶的方案数的和。很好理解,因为每次只能爬 1 级或 2 级,所以 f(x) 只能从 f(x - 1) 和 f(x - 2)转移过来,而这里要统计方案总数,我们就需要对这两项的贡献求和。
以上是动态规划的转移方程,下面我们来讨论边界条件。我们是从第 0 级开始爬的,所以从第 00 级爬到第 0 级我们可以看作只有一种方案,即 f(0) = 1;从第 0 级到第 1 级也只有一种方案,即爬一级,f(1) = 1。这两个作为边界条件就可以继续向后推导出第 n 级的正确结果。我们不妨写几项来验证一下,根据转移方程得到 f(2) = 2,f(3) = 3,f(4) = 5,……,我们把这些情况都枚举出来,发现计算的结果是正确的。
我们不难通过转移方程和边界条件给出一个时间复杂度和空间复杂度都是 O(n) 的实现,但是由于这里的 f(x) 只和 f(x - 1)与 f(x - 2) 有关,所以我们可以用「滚动数组思想」把空间复杂度优化成 O(1)。下面的代码中给出的就是这种实现。

1
2
3
4
5
6
7
8
9
10
11
| class Solution {
public int climbStairs(int n) {
int p = 0, q = 0, r = 1;
for (int i = 1; i <= n; ++i) {
p = q;
q = r;
r = p + q;
}
return r;
}
}
|
复杂度分析
- 时间复杂度:循环执行 n 次,每次花费常数的时间代价,故渐进时间复杂度为 O(n)。
- 空间复杂度:这里只用了常数个变量作为辅助空间,故渐进空间复杂度为 O(1)。
方法二:矩阵快速幂
思路
以上的方法适用于 n 比较小的情况,在 n 变大之后,O(n) 的时间复杂度会让这个算法看起来有些捉襟见肘。我们可以用「矩阵快速幂」的方法来优化这个过程。
首先我们可以构建这样一个递推关系:
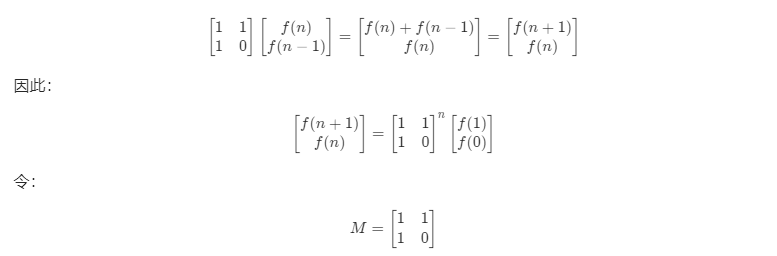


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| public class Solution {
public int climbStairs(int n) {
int[][] q = {{1, 1}, {1, 0}};
int[][] res = pow(q, n);
return res[0][0];
}
public int[][] pow(int[][] a, int n) {
int[][] ret = {{1, 0}, {0, 1}};
while (n > 0) {
if ((n & 1) == 1) {
ret = multiply(ret, a);
}
n >>= 1;
a = multiply(a, a);
}
return ret;
}
public int[][] multiply(int[][] a, int[][] b) {
int[][] c = new int[2][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];
}
}
return c;
}
}
|
复杂度分析
- 时间复杂度:同快速幂,O(logn*)。
- 空间复杂度:O*(1)。
方法三:通项公式
思路
之前的方法我们已经讨论了 f(n) 是齐次线性递推,根据递推方程 f(n)=f(n−1)+f(n−2),我们可以写出这样的特征方程:

1
2
3
4
5
6
7
| public class Solution {
public int climbStairs(int n) {
double sqrt5 = Math.sqrt(5);
double fibn = Math.pow((1 + sqrt5) / 2, n + 1) - Math.pow((1 - sqrt5) / 2, n + 1);
return (int) Math.round(fibn / sqrt5);
}
}
|
复杂度分析
代码中使用的 pow 函数的时空复杂度与 CPU 支持的指令集相关,这里不深入分析。
总结
这里形成的数列正好是斐波那契数列,答案要求的 f(n) 即是斐波那契数列的第 n 项(下标从 0 开始)。我们来总结一下斐波那契数列第 n 项的求解方法:
- n 比较小的时候,可以直接使用过递归法求解,不做任何记忆化操作,时间复杂度是 O(2^n),存在很多冗余计算。
- 一般情况下,我们使用「记忆化搜索」或者「迭代」的方法,实现这个转移方程,时间复杂度和空间复杂度都可以做到 O(n)O(n)。
- 为了优化空间复杂度,我们可以不用保存 f(x−2) 之前的项,我们只用三个变量来维护 f(x)、f(x−1) 和 f(x−2),你可以理解成是把「滚动数组思想」应用在了动态规划中,也可以理解成是一种递推,这样把空间复杂度优化到了 O(1)。
- 随着 n 的不断增大 O(n) 可能已经不能满足我们的需要了,我们可以用「矩阵快速幂」的方法把算法加速到 O(logn)。
- 我们也可以把 n 代入斐波那契数列的通项公式计算结果,但是如果我们用浮点数计算来实现,可能会产生精度误差。
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| 示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 400
|
方法一:动态规划
首先考虑最简单的情况。如果只有一间房屋,则偷窃该房屋,可以偷窃到最高总金额。如果只有两间房屋,则由于两间房屋相邻,不能同时偷窃,只能偷窃其中的一间房屋,因此选择其中金额较高的房屋进行偷窃,可以偷窃到最高总金额。
如果房屋数量大于两间,应该如何计算能够偷窃到的最高总金额呢?对于第 k (k>2) 间房屋,有两个选项:
偷窃第 k 间房屋,那么就不能偷窃第 k−1 间房屋,偷窃总金额为前 k−2 间房屋的最高总金额与第 k 间房屋的金额之和。
不偷窃第 k 间房屋,偷窃总金额为前 k−1 间房屋的最高总金额。
在两个选项中选择偷窃总金额较大的选项,该选项对应的偷窃总金额即为前 k 间房屋能偷窃到的最高总金额。
用 dp[i] 表示前 i 间房屋能偷窃到最高总金额,那么就有如下的状态转移方程:
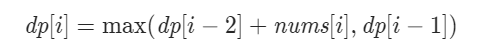


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int length = nums.length;
if (length == 1) {
return nums[0];
}
int[] dp = new int[length];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < length; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[length - 1];
}
}
|
上述方法使用了数组存储结果。考虑到每间房屋的最高总金额只和该房屋的前两间房屋的最高总金额相关,因此可以使用滚动数组,在每个时刻只需要存储前两间房屋的最高总金额。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int length = nums.length;
if (length == 1) {
return nums[0];
}
int first = nums[0], second = Math.max(nums[0], nums[1]);
for (int i = 2; i < length; i++) {
int temp = second;
second = Math.max(first + nums[i], second);
first = temp;
}
return second;
}
}
|
复杂度分析
- 时间复杂度:O(n),其中 n 是数组长度。只需要对数组遍历一次。
- 空间复杂度:O(1)。使用滚动数组,可以只存储前两间房屋的最高总金额,而不需要存储整个数组的结果,因此空间复杂度是 O(1)。
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| 示例1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例2:
输入:triangle = [[-10]]
输出:-10
提示:
1 <= triangle.length <= 200
triangle[0].length == 1
triangle[i].length == triangle[i - 1].length + 1
-104 <= triangle[i][j] <= 104
进阶:
你可以只使用 O(n) 的额外空间(n 为三角形的总行数)来解决这个问题吗?
|
前言
本题是一道非常经典且历史悠久的动态规划题,其作为算法题出现,最早可以追溯到 1994 年的 IOI(国际信息学奥林匹克竞赛)的 The Triangle。时光飞逝,经过 20 多年的沉淀,往日的国际竞赛题如今已经变成了动态规划的入门必做题,不断督促着我们学习和巩固算法。
在本题中,给定的三角形的行数为 n,并且第 i 行(从 00 开始编号)包含了 i+1 个数。如果将每一行的左端对齐,那么会形成一个等腰直角三角形,如下所示:
1
2
3
4
| [2]
[3,4]
[6,5,7]
[4,1,8,3]
|
方法一:动态规划
思路与算法



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int[][] f = new int[n][n];
f[0][0] = triangle.get(0).get(0);
for (int i = 1; i < n; ++i) {
f[i][0] = f[i - 1][0] + triangle.get(i).get(0);
for (int j = 1; j < i; ++j) {
f[i][j] = Math.min(f[i - 1][j - 1], f[i - 1][j]) + triangle.get(i).get(j);
}
f[i][i] = f[i - 1][i - 1] + triangle.get(i).get(i);
}
int minTotal = f[n - 1][0];
for (int i = 1; i < n; ++i) {
minTotal = Math.min(minTotal, f[n - 1][i]);
}
return minTotal;
}
}
|

方法二:动态规划 + 空间优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int[][] f = new int[2][n];
f[0][0] = triangle.get(0).get(0);
for (int i = 1; i < n; ++i) {
int curr = i % 2;
int prev = 1 - curr;
f[curr][0] = f[prev][0] + triangle.get(i).get(0);
for (int j = 1; j < i; ++j) {
f[curr][j] = Math.min(f[prev][j - 1], f[prev][j]) + triangle.get(i).get(j);
}
f[curr][i] = f[prev][i - 1] + triangle.get(i).get(i);
}
int minTotal = f[(n - 1) % 2][0];
for (int i = 1; i < n; ++i) {
minTotal = Math.min(minTotal, f[(n - 1) % 2][i]);
}
return minTotal;
}
}
|
上述方法的空间复杂度为 O(n),使用了 2n 的空间存储状态。我们还可以继续进行优化吗?
答案是可以的。我们从 i 到 0 递减地枚举j,这样我们只需要一个长度为 n 的一维数组 f,就可以完成状态转移。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int[] f = new int[n];
f[0] = triangle.get(0).get(0);
for (int i = 1; i < n; ++i) {
f[i] = f[i - 1] + triangle.get(i).get(i);
for (int j = i - 1; j > 0; --j) {
f[j] = Math.min(f[j - 1], f[j]) + triangle.get(i).get(j);
}
f[0] += triangle.get(i).get(0);
}
int minTotal = f[0];
for (int i = 1; i < n; ++i) {
minTotal = Math.min(minTotal, f[i]);
}
return minTotal;
}
}
|

结语
本题还有一些其它的动态规划方法,例如:
- 从三角形的底部开始转移,到顶部结束;
- 直接在给定的三角形数组上进行状态转移,不使用额外的空间。
读者可以自行尝试。如果在面试中遇到类似的题目,需要和面试官进行沟通,可以询问「是否有空间复杂度限制」「是否可以修改原数组」等问题,给出符合条件的算法。

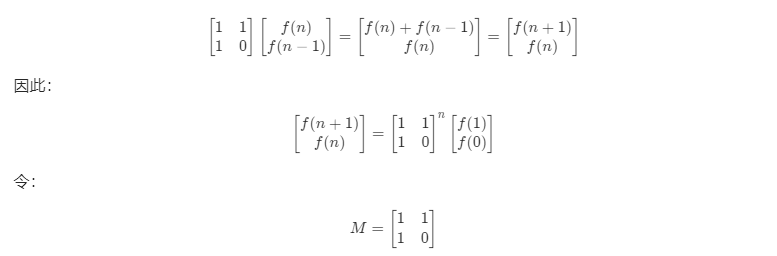



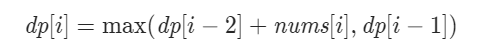









Copyright 2021 sunfy.top ALL Rights Reserved