算法常用的解题思路---位运算

Posted by Sunfy on 2021-08-27
Words 3k and Reading Time 11 Minutes
Viewed Times
Viewed Times
Visitors In Total

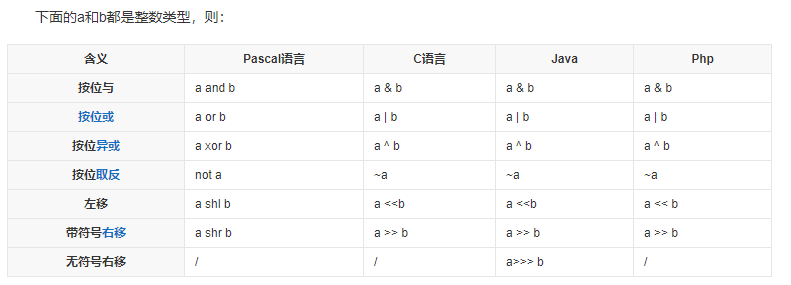
位运算

程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。比如，and运算本来是一个逻辑运算符，但整数与整数之间也可以进行and运算。举个例子，6的二进制是110，11的二进制是1011，那么6 and 11的结果就是2，它是二进制对应位进行逻辑运算的结果（0表示False，1表示True，空位都当0处理）。

image-20210827090511912

231. 2 的幂

给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。

如果存在一个整数 x 使得 n == 2^x ，则认为 n 是 2 的幂次方。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
示例 1：
输入：n = 1
输出：true
解释：20 = 1
示例 2：
输入：n = 16
输出：true
解释：24 = 16
示例 3：
输入：n = 3
输出：false
示例 4：
输入：n = 4
输出：true
示例 5：
输入：n = 5
输出：false
 
提示：
-2^31 <= n <= 2^31 - 1

方法一：二进制表示

image-20210827090843502

image-20210827090859357

image-20210827090914164

在一些语言中，位运算的优先级较低，需要注意运算顺序。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public boolean isPowerOfTwo(int n) {
        return n > 0 && (n & (n - 1)) == 0;
    }
}

class Solution {
    public boolean isPowerOfTwo(int n) {
        return n > 0 && (n & -n) == n;
    }
}

复杂度分析

  • 时间复杂度：O(1)。
  • 空间复杂度：O*(1)。

方法二：判断是否为最大 22 的幂的约数

思路与算法

除了使用二进制表示判断之外，还有一种较为取巧的做法。

在题目给定的 32 位有符号整数的范围内，最大的 2 的幂为 2^{30} = 1073741824 我们只需要判断 n 是否是 2^{30} 的约数即可。

1
2
3
4
5
6
7
class Solution {
    static final int BIG = 1 << 30;

    public boolean isPowerOfTwo(int n) {
        return n > 0 && BIG % n == 0;
    }
}

复杂度分析

  • 时间复杂度：O(1)。
  • 空间复杂度：O(1)。

191. 位1的个数

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。

提示：

  • 请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
  • 在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的 示例 3 中，输入表示有符号整数 -3。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
示例 1：
输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。
示例 2：
输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。
示例 3：
输入：11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 '1'。
 
提示：
输入必须是长度为 32 的 二进制串 。
 
进阶：
如果多次调用这个函数，你将如何优化你的算法？

方法一：循环检查二进制位

思路及解法

我们可以直接循环检查给定整数 n 的二进制位的每一位是否为 1。

具体代码中，当检查第 ii 位时，我们可以让 n 与 2^i 进行与运算，当且仅当 n 的第 i 位为 1 时，运算结果不为 0。

1
2
3
4
5
6
7
8
9
10
11
public class Solution {
    public int hammingWeight(int n) {
        int ret = 0;
        for (int i = 0; i < 32; i++) {
            if ((n & (1 << i)) != 0) {
                ret++;
            }
        }
        return ret;
    }
}

复杂度分析

  • 时间复杂度：O(k)，其中 k 是 int 型的二进制位数，k=32。我们需要检查 n 的二进制位的每一位，一共需要检查 32 位。
  • 空间复杂度：O(1)，我们只需要常数的空间保存若干变量。

方法二：位运算优化

思路及解法

观察这个运算：n~\&~(n - 1)，其运算结果恰为把 n 的二进制位中的最低位的 1 变为 0 之后的结果。

如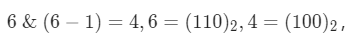：image-20210827091648500运算结果 4 即为把 6 的二进制位中的最低位的 1 变为 0 之后的结果。

这样我们可以利用这个位运算的性质加速我们的检查过程，在实际代码中，我们不断让当前的 n 与 n−1 做与运算，直到 n 变为 0 即可。因为每次运算会使得 n 的最低位的 1 被翻转，因此运算次数就等于 n 的二进制位中 1 的个数。

1
2
3
4
5
6
7
8
9
10
public class Solution {
    public int hammingWeight(int n) {
        int ret = 0;
        while (n != 0) {
            n &= n - 1;
            ret++;
        }
        return ret;
    }
}

复杂度分析

  • 时间复杂度：O(logn)。循环次数等于 n 的二进制位中 1 的个数，最坏情况下 n 的二进制位全部为 1。我们需要循环 logn 次。
  • 空间复杂度：O(1)，我们只需要常数的空间保存若干变量。

190. 颠倒二进制位

颠倒给定的 32 位无符号整数的二进制位。

提示：

  • 请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
  • 在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的 示例 2 中，输入表示有符号整数 -3，输出表示有符号整数 -1073741825。

进阶:
如果多次调用这个函数，你将如何优化你的算法？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
示例 1：
输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，
     因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。
示例 2：
输入：11111111111111111111111111111101
输出：10111111111111111111111111111111
解释：输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293，
     因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。
示例 3：
输入：n = 00000010100101000001111010011100
输出：964176192 (00111001011110000010100101000000)
解释：输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，
     因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。
示例 4：
输入：n = 11111111111111111111111111111101
输出：3221225471 (10111111111111111111111111111111)
解释：输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293，
     因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。

提示：
输入是一个长度为 32 的二进制字符串

方法一：逐位颠倒

思路

将 n 视作一个长为 32 的二进制串，从低位往高位枚举 n 的每一位，将其倒序添加到翻转结果 rev 中。

代码实现中，每枚举一位就将n 右移一位，这样当前 n 的最低位就是我们要枚举的比特位。当 n 为 0 时即可结束循环。

需要注意的是，在某些语言（如 Java）中，没有无符号整数类型，因此对 n 的右移操作应使用逻辑右移。

1
2
3
4
5
6
7
8
9
10
public class Solution {
    public int reverseBits(int n) {
        int rev = 0;
        for (int i = 0; i < 32 && n != 0; ++i) {
            rev |= (n & 1) << (31 - i);
            n >>>= 1;
        }
        return rev;
    }
}

复杂度分析

  • 时间复杂度：O(logn)。
  • 空间复杂度：O(1)。

方法二：位运算分治

思路

若要翻转一个二进制串，可以将其均分成左右两部分，对每部分递归执行翻转操作，然后将左半部分拼在右半部分的后面，即完成了翻转。

由于左右两部分的计算方式是相似的，利用位掩码和位移运算，我们可以自底向上地完成这一分治流程。

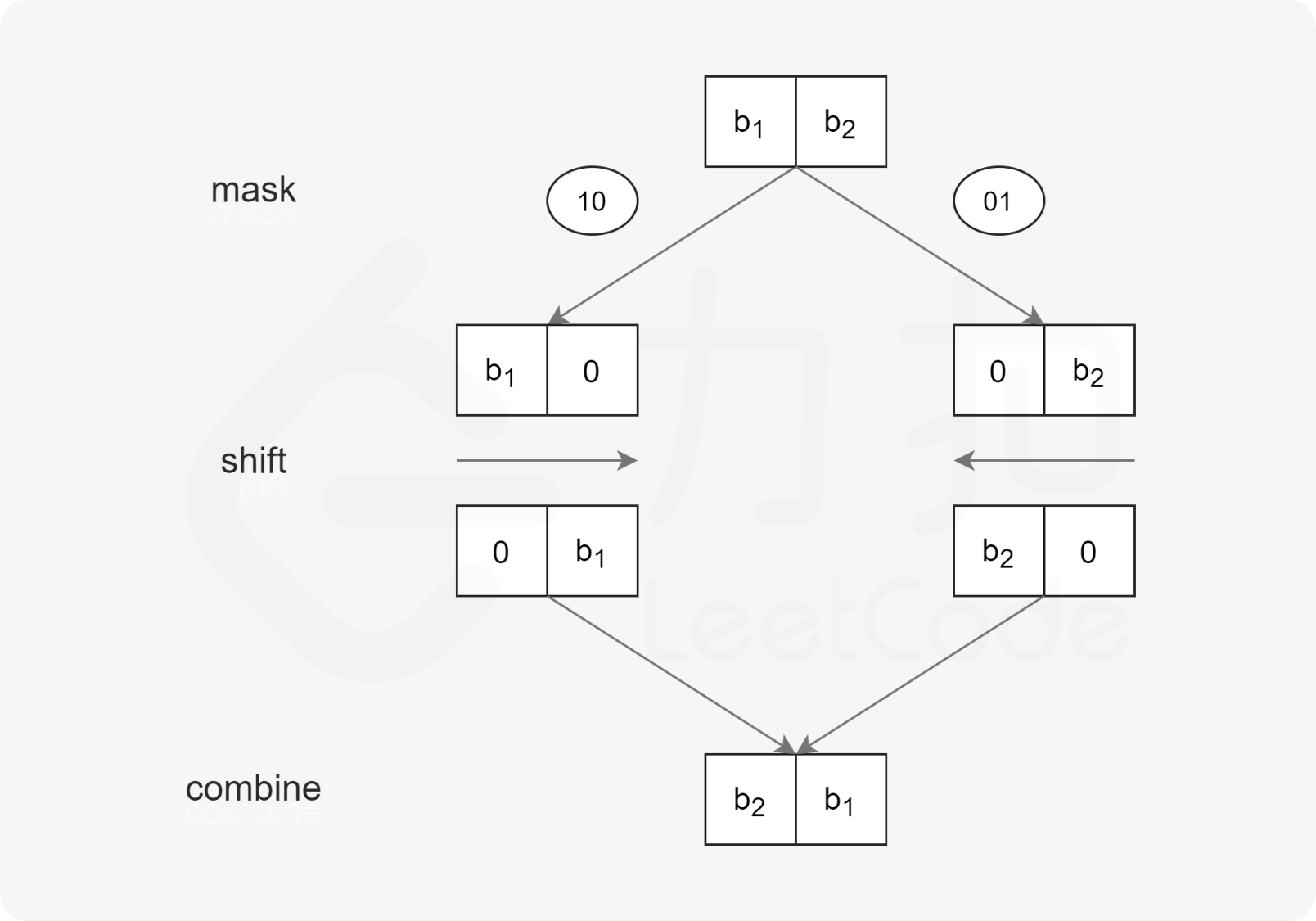
190_fig1

对于递归的最底层，我们需要交换所有奇偶位：

  • 取出所有奇数位和偶数位；
  • 将奇数位移到偶数位上，偶数位移到奇数位上。

类似地，对于倒数第二层，每两位分一组，按组号取出所有奇数组和偶数组，然后将奇数组移到偶数组上，偶数组移到奇数组上。以此类推。

需要注意的是，在某些语言（如Java）中，没有无符号整数类型，因此对 n 的右移操作应使用逻辑右移。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class Solution {
    private static final int M1 = 0x55555555; // 01010101010101010101010101010101
    private static final int M2 = 0x33333333; // 00110011001100110011001100110011
    private static final int M4 = 0x0f0f0f0f; // 00001111000011110000111100001111
    private static final int M8 = 0x00ff00ff; // 00000000111111110000000011111111

    public int reverseBits(int n) {
        n = n >>> 1 & M1 | (n & M1) << 1;
        n = n >>> 2 & M2 | (n & M2) << 2;
        n = n >>> 4 & M4 | (n & M4) << 4;
        n = n >>> 8 & M8 | (n & M8) << 8;
        return n >>> 16 | n << 16;
    }
}

复杂度分析

  • 时间复杂度：O(1)。
  • 空间复杂度：O(1)。

136. 只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

1
2
3
4
5
6
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4

方法一：位运算

如果不考虑时间复杂度和空间复杂度的限制，这道题有很多种解法，可能的解法有如下几种。

使用集合存储数字。遍历数组中的每个数字，如果集合中没有该数字，则将该数字加入集合，如果集合中已经有该数字，则将该数字从集合中删除，最后剩下的数字就是只出现一次的数字。

使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数，并更新哈希表，最后遍历哈希表，得到只出现一次的数字。

使用集合存储数组中出现的所有数字，并计算数组中的元素之和。由于集合保证元素无重复，因此计算集合中的所有元素之和的两倍，即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次，其余元素都出现两次，因此用集合中的元素之和的两倍减去数组中的元素之和，剩下的数就是数组中只出现一次的数字。

上述三种解法都需要额外使用 O(n) 的空间，其中 n是数组长度。

如何才能做到线性时间复杂度和常数空间复杂度呢？

答案是使用位运算。对于这道题，可使用异或运算 ⊕。异或运算有以下三个性质。

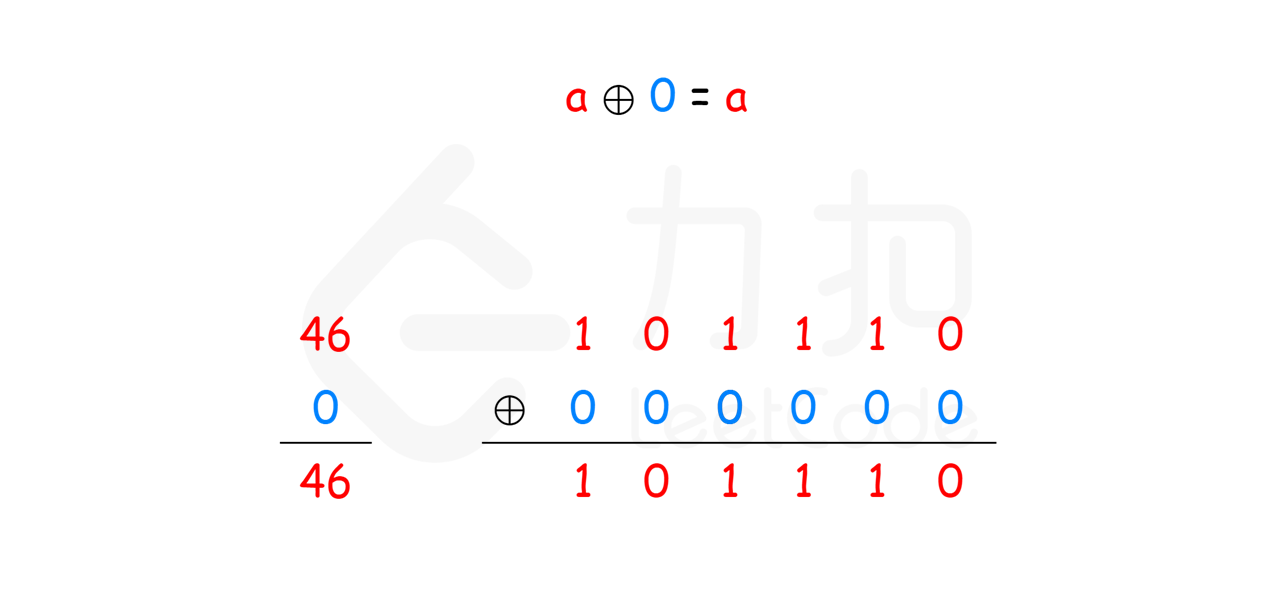
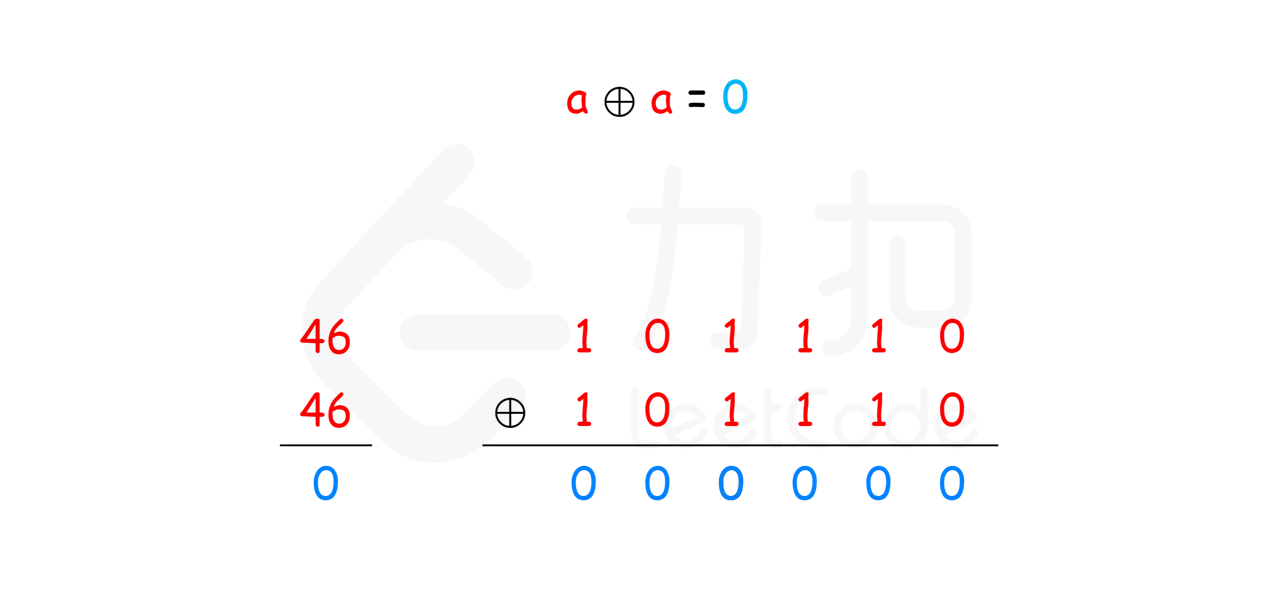
  1. 任何数和 0 做异或运算，结果仍然是原来的数，即 a⊕0=a。
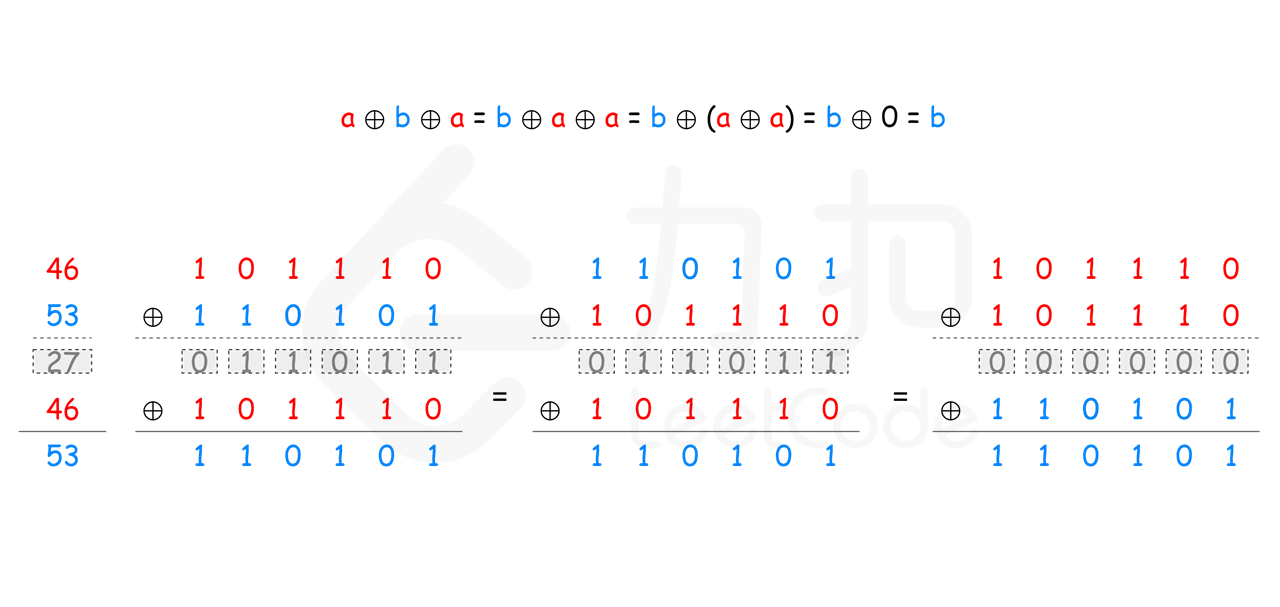
  2. 任何数和其自身做异或运算，结果是 0，即 a⊕a=0。
  3. 异或运算满足交换律和结合律，即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。

1

2

3

假设数组中有 2m+1 个数，其中有 m 个数各出现两次，一个数出现一次。令 a1、a2、…、am为出现两次的 m 个数，a
m+1 为出现一次的数。根据性质 3，数组中的全部元素的异或运算结果总是可以写成如下形式：

(a1⊕a1)⊕(a2⊕a2)⊕⋯⊕(am⊕am)⊕am+1

根据性质 2 和性质 1，上式可化简和计算得到如下结果：

0⊕0⊕⋯⊕0⊕am+1=am+1

因此，数组中的全部元素的异或运算结果即为数组中只出现一次的数字。

1
2
3
4
5
6
7
8
9
class Solution {
    public int singleNumber(int[] nums) {
        int single = 0;
        for (int num : nums) {
            single ^= num;
        }
        return single;
    }
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 是数组长度。只需要对数组遍历一次。
  • 空间复杂度：O(1)。

Copyright 2021 sunfy.top ALL Rights Reserved

...

...

00:00
00:00
FEATURED TAGS
FRIENDS