217. 存在重复元素
给定一个整数数组,判断是否存在重复元素。
如果存在一值在数组中出现至少两次,函数返回 true 。如果数组中每个元素都不相同,则返回 false 。
1 | 示例 1: |
方法一:排序
在对数字从小到大排序之后,数组的重复元素一定出现在相邻位置中。因此,我们可以扫描已排序的数组,每次判断相邻的两个元素是否相等,如果相等则说明存在重复的元素。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(NlogN),其中N为数组的长度。需要对数组进行排序。 - 空间复杂度:
O(logN),其中N为数组的长度。注意我们在这里应当考虑递归调用栈的深度。
方法二:哈希表
对于数组中每个元素,我们将它插入到哈希表中。如果插入一个元素时发现该元素已经存在于哈希表中,则说明存在重复的元素。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(N),其中N为数组的长度。 - 空间复杂度:
O(N),其中N为数组的长度。
53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
1 | 示例 1: |
方法一:贪心算法
方法二:动态规划

1 | class Solution { |
复杂度
- 时间复杂度:
O(n),其中n为nums数组的长度。我们只需要遍历一遍数组即可求得答案。 - 空间复杂度:
O(1)。我们只需要常数空间存放若干变量。
方法三:分治



1 | class Solution { |

番外篇
「方法三」相较于「方法二」来说,时间复杂度相同,但是因为使用了递归,并且维护了四个信息的结构体,运行的时间略长,空间复杂度也不如方法一优秀,而且难以理解。那么这种方法存在的意义是什么呢?
对于这道题而言,确实是如此的。但是仔细观察「方法三」,它不仅可以解决区间 [0,n−1],还可以用于解决任意的子区间 [l,r] 的问题。如果我们把 [0, n-1] 分治下去出现的所有子区间的信息都用堆式存储的方式记忆化下来,即建成一颗真正的树之后,我们就可以在 O(logn) 的时间内求到任意区间内的答案,我们甚至可以修改序列中的值,做一些简单的维护,之后仍然可以在 O(logn) 的时间内求到任意区间内的答案,对于大规模查询的情况下,这种方法的优势便体现了出来。这棵树就是上文提及的一种神奇的数据结构——线段树。
1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
1 | 示例 1: |
进阶:你可以想出一个时间复杂度小于 O(n^2) 的算法吗?
方法一:暴力枚举
思路及算法
最容易想到的方法是枚举数组中的每一个数 x,寻找数组中是否存在 target - x。
当我们使用遍历整个数组的方式寻找 target - x 时,需要注意到每一个位于 x 之前的元素都已经和 x 匹配过,因此不需要再进行匹配。而每一个元素不能被使用两次,所以我们只需要在 x 后面的元素中寻找 target - x。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(N^2),其中N是数组中的元素数量。最坏情况下数组中任意两个数都要被匹配一次。 - 空间复杂度:
O(1)。
方法二:哈希表
思路及算法
注意到方法一的时间复杂度较高的原因是寻找 target - x 的时间复杂度过高。因此,我们需要一种更优秀的方法,能够快速寻找数组中是否存在目标元素。如果存在,我们需要找出它的索引。
使用哈希表,可以将寻找 target - x 的时间复杂度降低到从 O(N) 降低到 O(1)。
这样我们创建一个哈希表,对于每一个 x,我们首先查询哈希表中是否存在 target - x,然后将 x 插入到哈希表中,即可保证不会让 x 和自己匹配。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(N),其中N是数组中的元素数量。对于每一个元素 x,我们可以O(1)地寻找 target - x。 - 空间复杂度:
O(N),其中N是数组中的元素数量。主要为哈希表的开销。
88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
1 | 示例 1: |
进阶:你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
方法一:直接合并后排序
算法
最直观的方法是先将数组 nums2 放进数组 nums1 的尾部,然后直接对整个数组进行排序。
1 | class Solution { |
复杂度分析
时间复杂度:
O((m+n)log(m+n))。
排序序列长度为m+n,套用快速排序的时间复杂度即可,平均情况为O((m+n)log(m+n))。空间复杂度:
O(log(m+n))。
排序序列长度为m+n,套用快速排序的空间复杂度即可,平均情况为O(log(m+n))。
方法二:双指针
算法
方法一没有利用数组 nums1与 nums2 已经被排序的性质。为了利用这一性质,我们可以使用双指针方法。这一方法将两个数组看作队列,每次从两个数组头部取出比较小的数字放到结果中。如下面的动画所示:
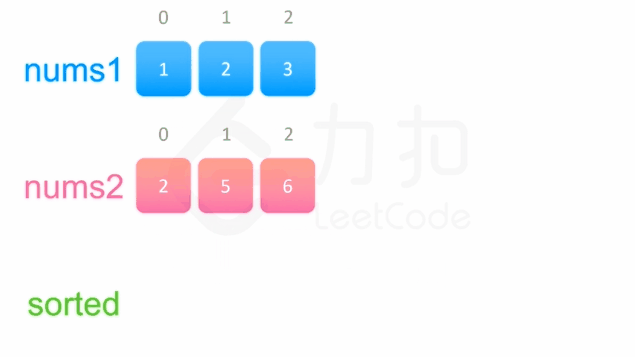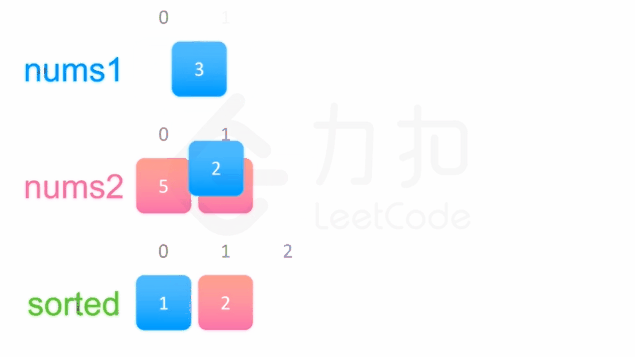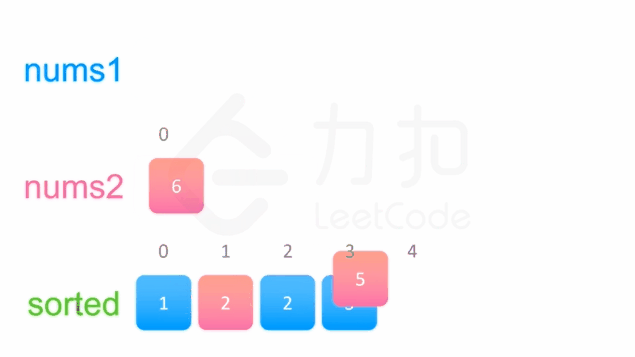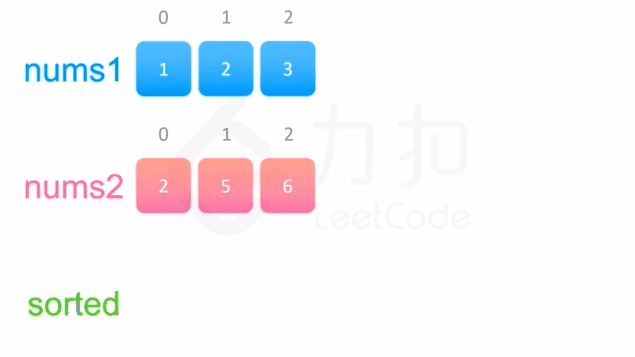
我们为两个数组分别设置一个指针 p1 与 p2 来作为队列的头部指针。代码实现如下:
1 | class Solution { |
复杂度分析
时间复杂度:
O(m+n)。
指针移动单调递增,最多移动m+n次,因此时间复杂度为O(m+n)。空间复杂度:
O(m+n)。
需要建立长度为m+n的中间数组sorted。
方法三:逆向双指针

1 | class Solution { |
复杂度分析
时间复杂度:
O(m+n)。
指针移动单调递减,最多移动m+n次,因此时间复杂度为O(m+n)。空间复杂度:
O(1)。
直接对数组nums1原地修改,不需要额外空间。
350. 两个数组的交集 II
给定两个数组,编写一个函数来计算它们的交集。
1 | 示例 1: |
说明:
- 输出结果中每个元素出现的次数,应与元素在两个数组中出现次数的最小值一致。
- 我们可以不考虑输出结果的顺序。
进阶:
- 如果给定的数组已经排好序呢?你将如何优化你的算法?
- 如果
nums1的大小比nums2小很多,哪种方法更优? - 如果
nums2的元素存储在磁盘上,内存是有限的,并且你不能一次加载所有的元素到内存中,你该怎么办?
方法一:哈希表
由于同一个数字在两个数组中都可能出现多次,因此需要用哈希表存储每个数字出现的次数。对于一个数字,其在交集中出现的次数等于该数字在两个数组中出现次数的最小值。
首先遍历第一个数组,并在哈希表中记录第一个数组中的每个数字以及对应出现的次数,然后遍历第二个数组,对于第二个数组中的每个数字,如果在哈希表中存在这个数字,则将该数字添加到答案,并减少哈希表中该数字出现的次数。
为了降低空间复杂度,首先遍历较短的数组并在哈希表中记录每个数字以及对应出现的次数,然后遍历较长的数组得到交集。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(m+n),其中m和n分别是两个数组的长度。需要遍历两个数组并对哈希表进行操作,哈希表操作的时间复杂度是O(1),因此总时间复杂度与两个数组的长度和呈线性关系。
- 空间复杂度:
O(min(m,n)),其中m和n分别是两个数组的长度。对较短的数组进行哈希表的操作,哈希表的大小不会超过较短的数组的长度。为返回值创建一个数组intersection,其长度为较短的数组的长度。
方法二:排序 + 双指针
如果两个数组是有序的,则可以使用双指针的方法得到两个数组的交集。
首先对两个数组进行排序,然后使用两个指针遍历两个数组。
初始时,两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字,如果两个数字不相等,则将指向较小数字的指针右移一位,如果两个数字相等,将该数字添加到答案,并将两个指针都右移一位。当至少有一个指针超出数组范围时,遍历结束。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(mlogm+nlogn),其中m和n分别是两个数组的长度。对两个数组进行排序的时间复杂度是O(mlogm+nlogn),遍历两个数组的时间复杂度是O(m+n),因此总时间复杂度是O(mlogm+nlogn)。 - 空间复杂度:
O(min(m,n)),其中m和n分别是两个数组的长度。为返回值创建一个数组intersection,其长度为较短的数组的长度。不过在 C++ 中,我们可以直接创建一个vector,不需要把答案临时存放在一个额外的数组中,所以这种实现的空间复杂度为O(1)。
结语
如果 nums2 的元素存储在磁盘上,磁盘内存是有限的,并且你不能一次加载所有的元素到内存中。那么就无法高效地对 nums2 进行排序,因此推荐使用方法一而不是方法二。在方法一中,nums2 只关系到查询操作,因此每次读取nums2 中的一部分数据,并进行处理即可。
121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
1 | 示例 1: |
解决方案
我们需要找出给定数组中两个数字之间的最大差值(即,最大利润)。此外,第二个数字(卖出价格)必须大于第一个数字(买入价格)。
形式上,对于每组 i 和 j(其中 j > i)我们需要找出 max(prices[j]−prices[i])。
方法一:暴力法
1 | public class Solution { |

方法二:一次遍历
算法
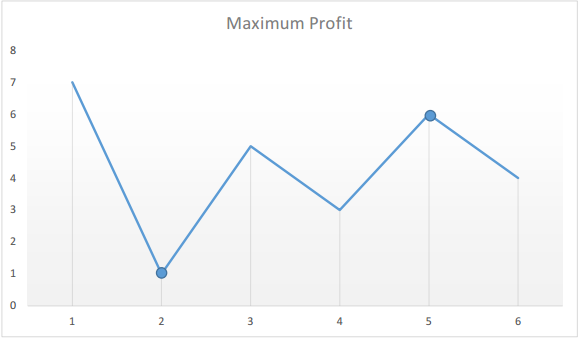
假设给定的数组为:[7, 1, 5, 3, 6, 4]
如果我们在图表上绘制给定数组中的数字,我们将会得到:
我们来假设自己来购买股票。随着时间的推移,每天我们都可以选择出售股票与否。那么,假设在第 i 天,如果我们要在今天卖股票,那么我们能赚多少钱呢?
显然,如果我们真的在买卖股票,我们肯定会想:如果我是在历史最低点买的股票就好了!太好了,在题目中,我们只要用一个变量记录一个历史最低价格 minprice,我们就可以假设自己的股票是在那天买的。那么我们在第 i 天卖出股票能得到的利润就是 prices[i] - minprice。
因此,我们只需要遍历价格数组一遍,记录历史最低点,然后在每一天考虑这么一个问题:如果我是在历史最低点买进的,那么我今天卖出能赚多少钱?当考虑完所有天数之时,我们就得到了最好的答案。
1 | public class Solution { |
复杂度分析
- 时间复杂度:
O(n),只需要遍历一次。 - 空间复杂度:
O(1),只使用了常数个变量。
566. 重塑矩阵
在 MATLAB 中,有一个非常有用的函数 reshape ,它可以将一个 m x n 矩阵重塑为另一个大小不同(r x c)的新矩阵,但保留其原始数据。
给你一个由二维数组 mat 表示的 m x n 矩阵,以及两个正整数 r 和 c ,分别表示想要的重构的矩阵的行数和列数。
重构后的矩阵需要将原始矩阵的所有元素以相同的 行遍历顺序 填充。
如果具有给定参数的 reshape 操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
示例 1:
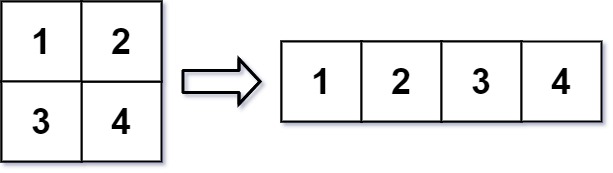
1 | 输入:mat = [[1,2],[3,4]], r = 1, c = 4 |
示例 2:
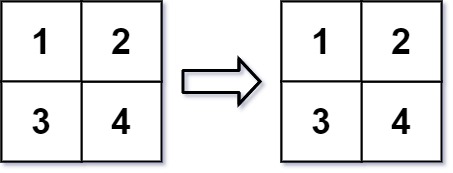
1 | 输入:mat = [[1,2],[3,4]], r = 2, c = 4 |
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 100-1000 <= mat[i][j] <= 10001 <= r, c <= 300
方法一:二维数组的一维表示

1 | class Solution { |
复杂度分析
- 时间复杂度:
O(rc)。这里的时间复杂度是在重塑矩阵成功的前提下的时间复杂度,否则当mn/rc时,C++ 语言中返回的是原数组的一份拷贝,本质上需要的时间复杂度为O(mn),而其余语言可以直接返回原数组的对象,需要的时间复杂度仅为O(1)。 - 空间复杂度:
O(1)。这里的空间复杂度不包含返回的重塑矩阵需要的空间。
118. 杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
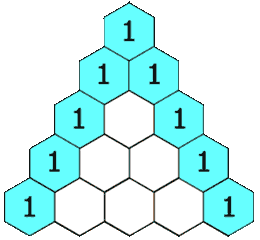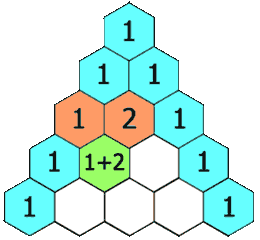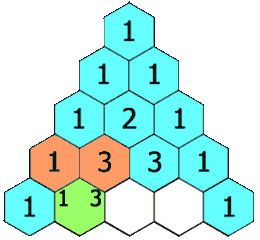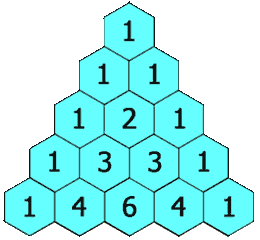
1 | 示例 1: |
方法一:数学

1 | class Solution { |
复杂度分析
- 时间复杂度:
O(numRows2)。 - 空间复杂度:
O(1)。不考虑返回值的空间占用。
36. 有效的数独
请你判断一个 9x9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的
3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
注意:
一个有效的数独(部分已被填充)不一定是可解的。
只需要根据以上规则,验证已经填入的数字是否有效即可。
示例 1:

1 | 输入:board = |
思路
一个简单的解决方案是遍历该 9 x 9 数独 三 次,以确保:
- 行中没有重复的数字。
- 列中没有重复的数字。
3 x 3子数独内没有重复的数字。
实际上,所有这一切都可以在一次迭代中完成。
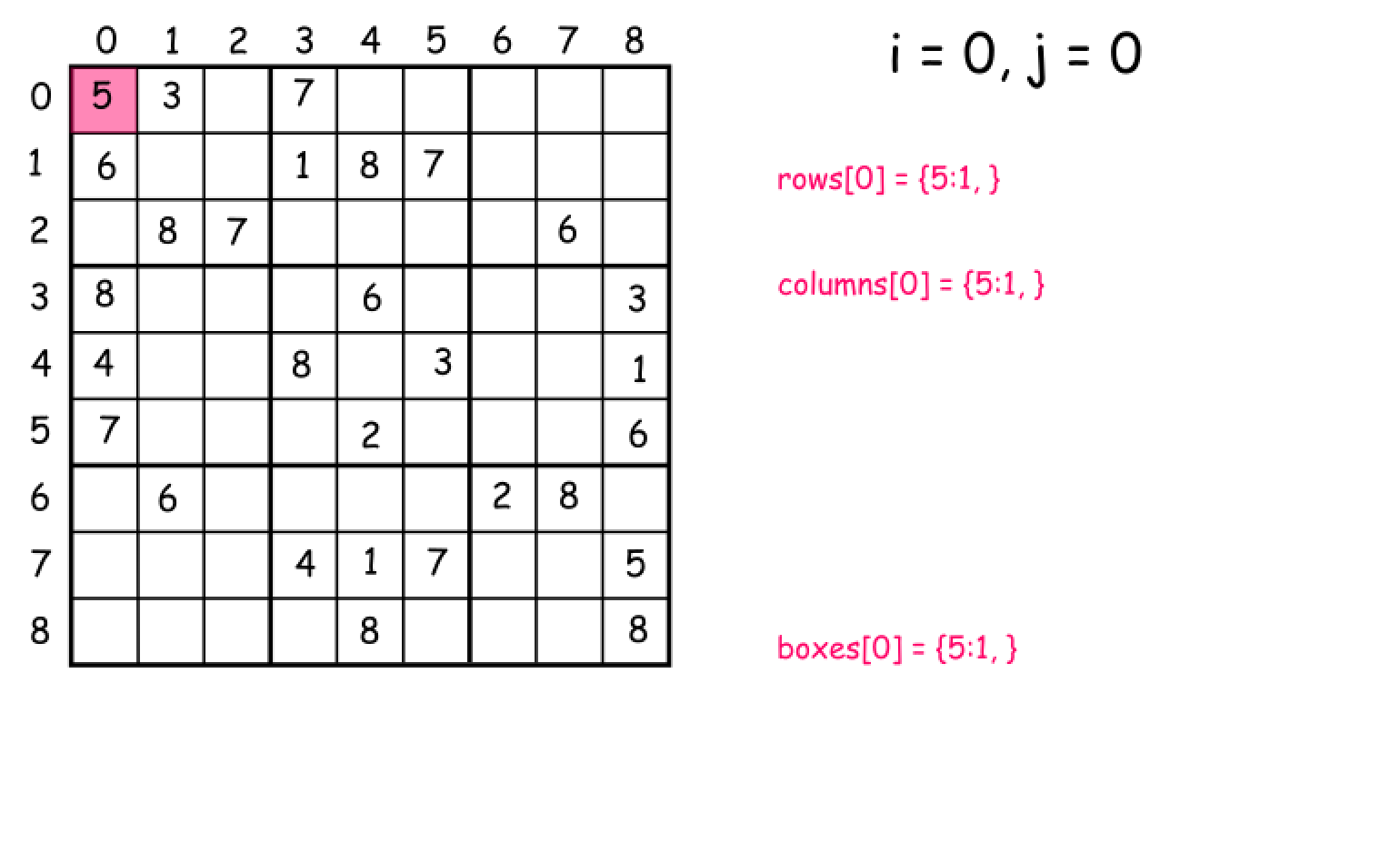
方法:一次迭代
首先,让我们来讨论下面两个问题:
如何枚举子数独?
可以使用
box_index = (row / 3) * 3 + columns / 3,其中 / 是整数除法。
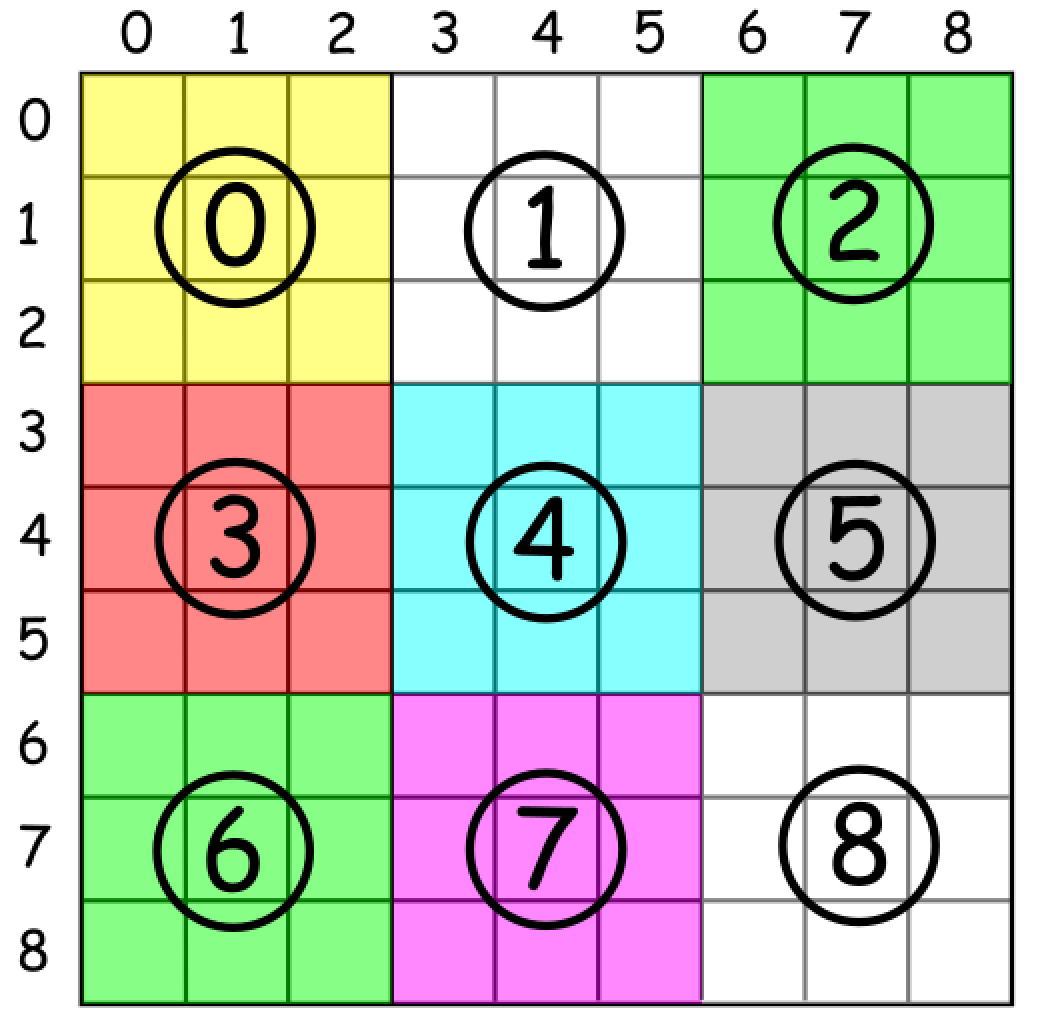
- 如何确保行 / 列 / 子数独中没有重复项?
可以利用
value -> count哈希映射来跟踪所有已经遇到的值。
现在,我们完成了这个算法的所有准备工作:
- 遍历数独。
- 检查看到每个单元格值是否已经在当前的行 / 列 / 子数独中出现过:
- 如果出现重复,返回 false。
- 如果没有,则保留此值以进行进一步跟踪。
- 返回 true。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(1),因为我们只对81个单元格进行了一次迭代。 - 空间复杂度:
O(1)
73. 矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
进阶:
- 一个直观的解决方案是使用
O(mn)的额外空间,但这并不是一个好的解决方案。 - 一个简单的改进方案是使用
O(m + n)的额外空间,但这仍然不是最好的解决方案。 - 你能想出一个仅使用常量空间的解决方案吗?
1 | 示例 1: |
方法一:使用标记数组
思路和算法
我们可以用两个标记数组分别记录每一行和每一列是否有零出现。
具体地,我们首先遍历该数组一次,如果某个元素为 0,那么就将该元素所在的行和列所对应标记数组的位置置为 true。最后我们再次遍历该数组,用标记数组更新原数组即可。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(mn),其中m是矩阵的行数,n是矩阵的列数。我们至多只需要遍历该矩阵两次。 - 空间复杂度:
O(m+n),其中m是矩阵的行数,n是矩阵的列数。我们需要分别记录每一行或每一列是否有零出现。
方法二:使用两个标记变量
思路和算法
我们可以用矩阵的第一行和第一列代替方法一中的两个标记数组,以达到 O(1) 的额外空间。但这样会导致原数组的第一行和第一列被修改,无法记录它们是否原本包含 0。因此我们需要额外使用两个标记变量分别记录第一行和第一列是否原本包含 0。
在实际代码中,我们首先预处理出两个标记变量,接着使用其他行与列去处理第一行与第一列,然后反过来使用第一行与第一列去更新其他行与列,最后使用两个标记变量更新第一行与第一列即可。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(mn),其中m是矩阵的行数,n是矩阵的列数。我们至多只需要遍历该矩阵两次。 - 空间复杂度:
O(1)。我们只需要常数空间存储若干变量。
方法三:使用一个标记变量
思路和算法
我们可以对方法二进一步优化,只使用一个标记变量记录第一列是否原本存在 0。这样,第一列的第一个元素即可以标记第一行是否出现 0。但为了防止每一列的第一个元素被提前更新,我们需要从最后一行开始,倒序地处理矩阵元素。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(mn),其中m是矩阵的行数,n是矩阵的列数。我们至多只需要遍历该矩阵两次。 - 空间复杂度:
O(1)。我们只需要常数空间存储若干变量。
...
...
Copyright 2021 sunfy.top ALL Rights Reserved