144. 二叉树的前序遍历
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
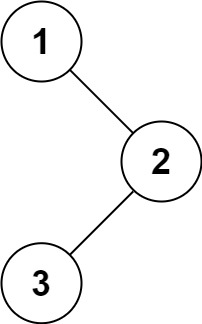
1 | 输入:root = [1,null,2,3] |
示例 4:
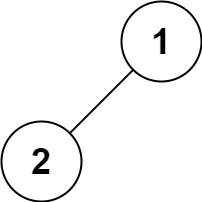
1 | 输入:root = [1,2] |
示例 5:
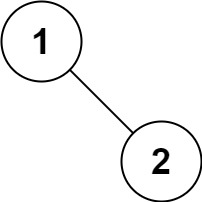
1 | 输入:root = [1,null,2] |
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
进阶:递归算法很简单,你可以通过迭代算法完成吗?
方法一:递归

1 | class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中n是二叉树的节点数。每一个节点恰好被遍历一次。 - 空间复杂度:
O(n),为递归过程中栈的开销,平均情况下为O(logn),最坏情况下树呈现链状,为O(n)。
方法二:迭代
思路与算法
我们也可以用迭代的方式实现方法一的递归函数,两种方式是等价的,区别在于递归的时候隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来,其余的实现与细节都相同,具体可以参考下面的代码。
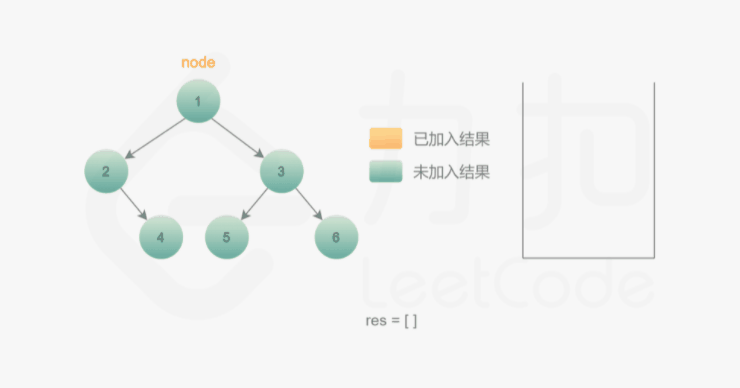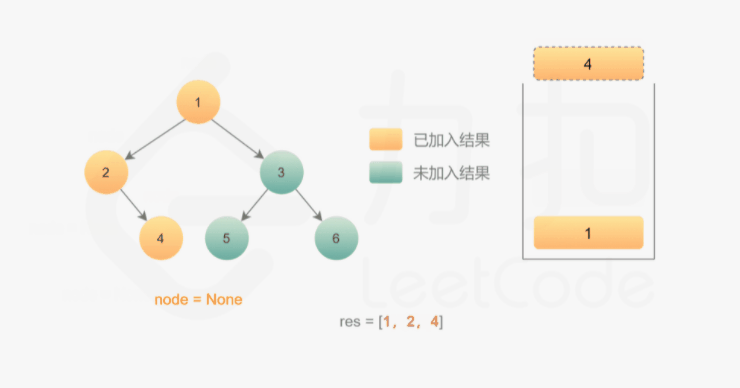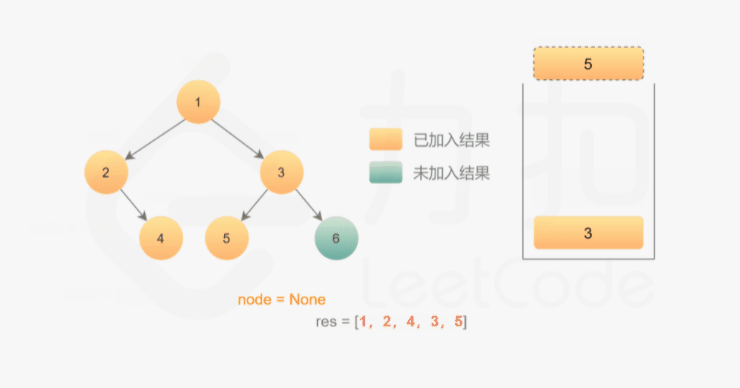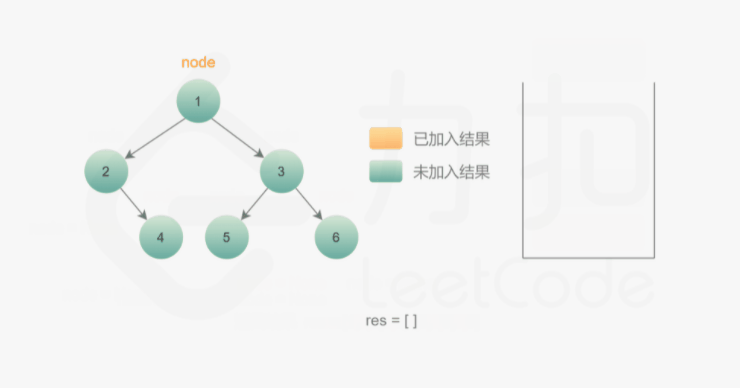
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中n是二叉树的节点数。每一个节点恰好被遍历一次。 - 空间复杂度:
O(n),为迭代过程中显式栈的开销,平均情况下为O(logn),最坏情况下树呈现链状,为O(n)。
方法三:Morris 遍历
思路与算法
有一种巧妙的方法可以在线性时间内,只占用常数空间来实现前序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出,因此被称为 Morris 遍历。
Morris 遍历的核心思想是利用树的大量空闲指针,实现空间开销的极限缩减。其前序遍历规则总结如下:
- 新建临时节点,令该节点为 root;
- 如果当前节点的左子节点为空,将当前节点加入答案,并遍历当前节点的右子节点;
如果当前节点的左子节点不为空,在当前节点的左子树中找到当前节点在中序遍历下的前驱节点:
- 如果前驱节点的右子节点为空,将前驱节点的右子节点设置为当前节点。然后将当前节点加入答案,并将前驱节点的右子节点更新为当前节点。当前节点更新为当前节点的左子节点。
- 如果前驱节点的右子节点为当前节点,将它的右子节点重新设为空。当前节点更新为当前节点的右子节点。
重复步骤 2 和步骤 3,直到遍历结束。
这样我们利用 Morris 遍历的方法,前序遍历该二叉树,即可实现线性时间与常数空间的遍历。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中n是二叉树的节点数。没有左子树的节点只被访问一次,有左子树的节点被访问两次。 - 空间复杂度:
O(1)。只操作已经存在的指针(树的空闲指针),因此只需要常数的额外空间。
94. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回它的 中序 遍历。
示例 1:
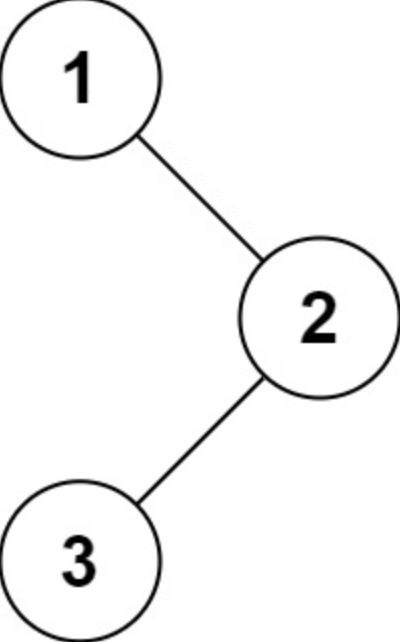
1 | 输入:root = [1,null,2,3] |
示例 4:
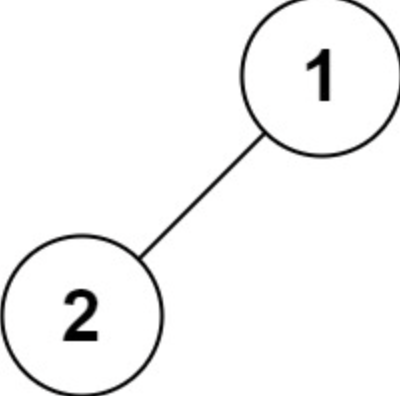
1 | 输入:root = [1,2] |
示例 5:
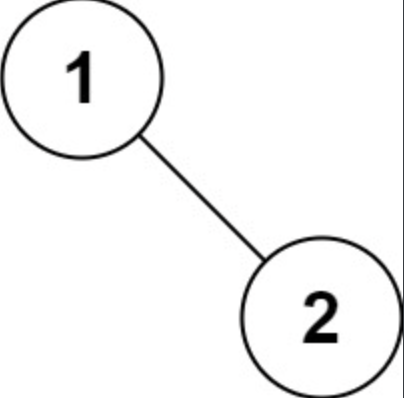
1 | 输入:root = [1,null,2] |
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
进阶:递归算法很简单,你可以通过迭代算法完成吗?
方法一:递归

1 | class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中n为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。 - 空间复杂度:
O(n)。空间复杂度取决于递归的栈深度,而栈深度在二叉树为一条链的情况下会达到O(n)的级别。
方法二:迭代
思路与算法
方法一的递归函数我们也可以用迭代的方式实现,两种方式是等价的,区别在于递归的时候隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来,其他都相同,具体实现可以看下面的代码。
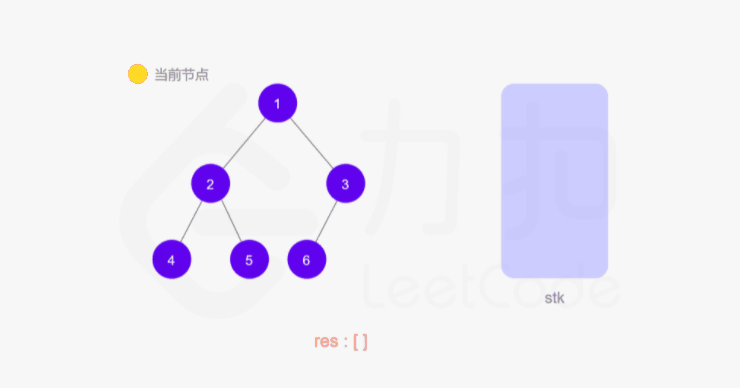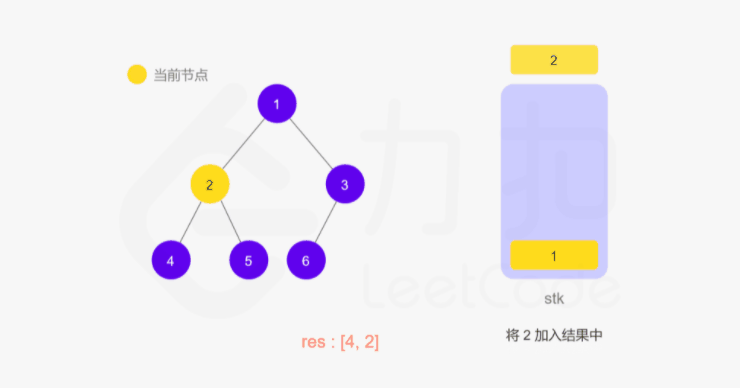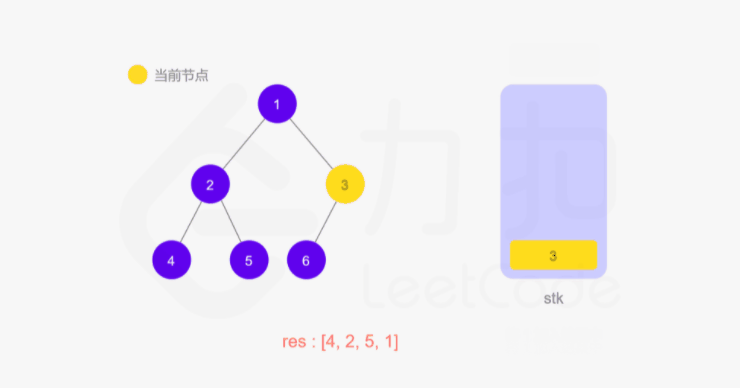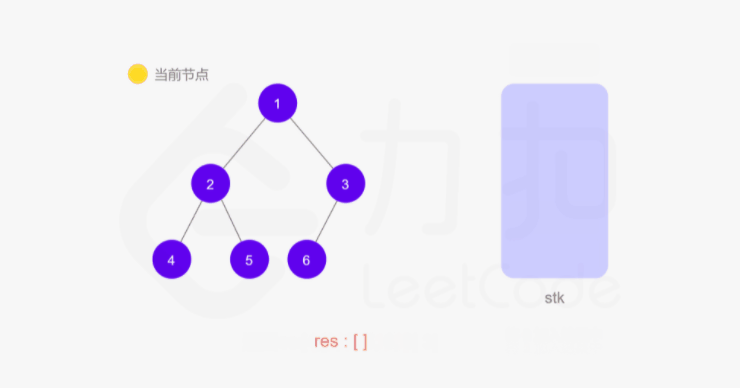
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中n为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。 - 空间复杂度:
O(n)。空间复杂度取决于栈深度,而栈深度在二叉树为一条链的情况下会达到O(n)的级别。
方法三:Morris 中序遍历

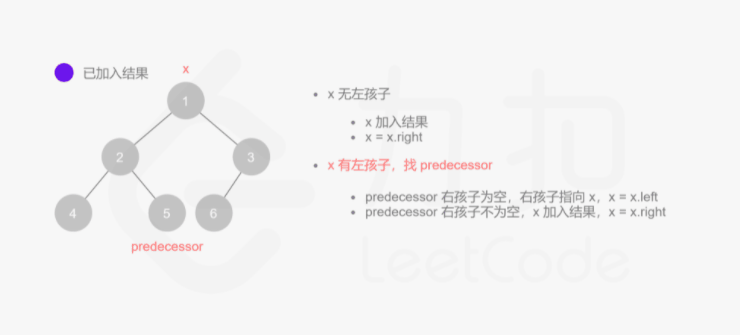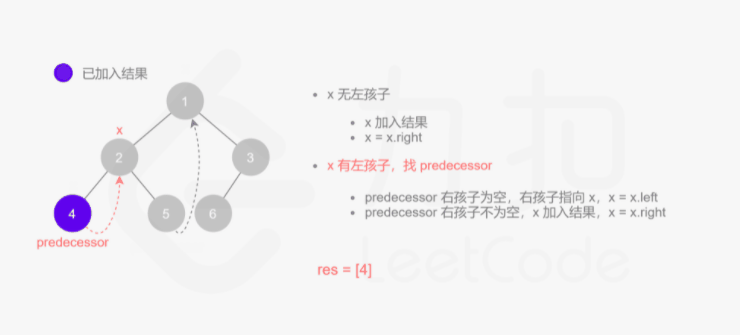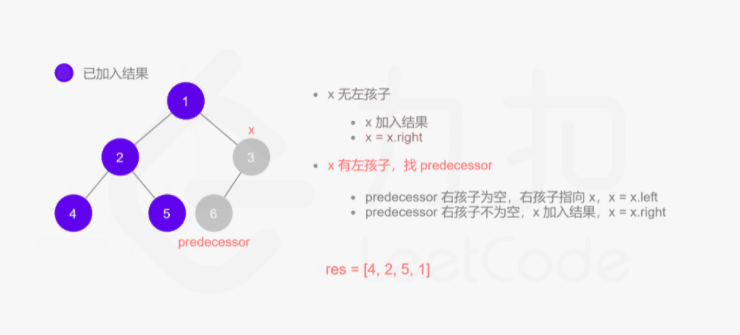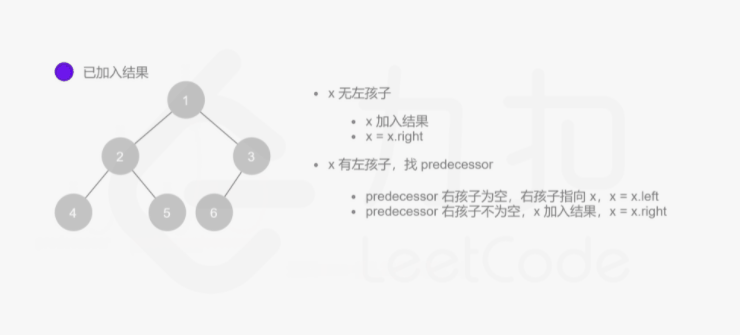
其实整个过程我们就多做一步:假设当前遍历到的节点为 x,将 x 的左子树中最右边的节点的右孩子指向 x,这样在左子树遍历完成后我们通过这个指向走回了 x,且能通过这个指向知晓我们已经遍历完成了左子树,而不用再通过栈来维护,省去了栈的空间复杂度。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中n为二叉搜索树的节点个数。Morris 遍历中每个节点会被访问两次,因此总时间复杂度为O(2n)=O(n)。 - 空间复杂度:
O(1)。
145. 二叉树的后序遍历
给定一个二叉树,返回它的 后序 遍历。
1 | 示例 |
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
方法一:递归

1 | class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中n是二叉搜索树的节点数。每一个节点恰好被遍历一次。 - 空间复杂度:
O(n),为递归过程中栈的开销,平均情况下为O(logn),最坏情况下树呈现链状,为O(n)。
方法二:迭代
思路与算法
我们也可以用迭代的方式实现方法一的递归函数,两种方式是等价的,区别在于递归的时候隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来,其余的实现与细节都相同,具体可以参考下面的代码。
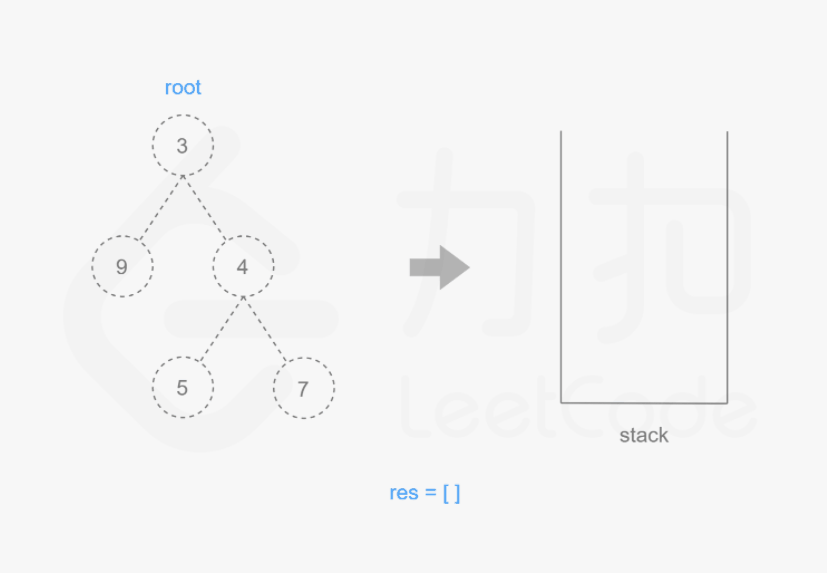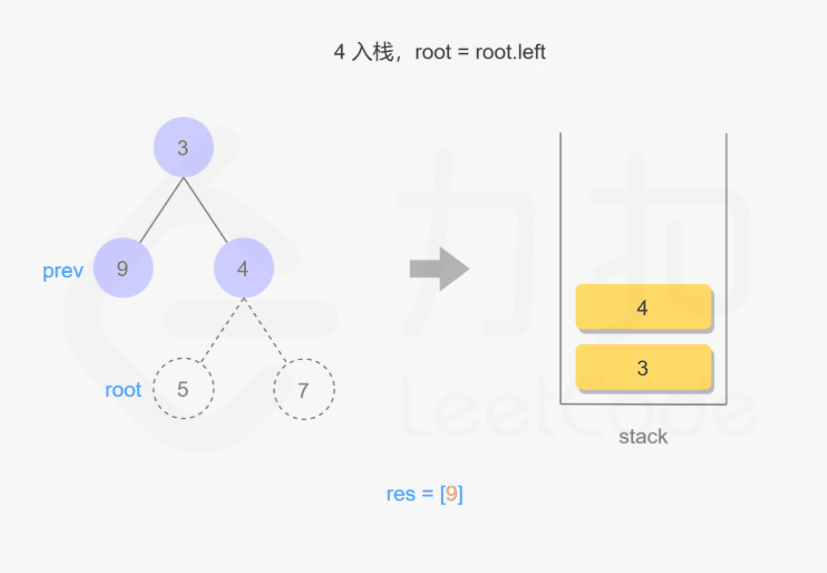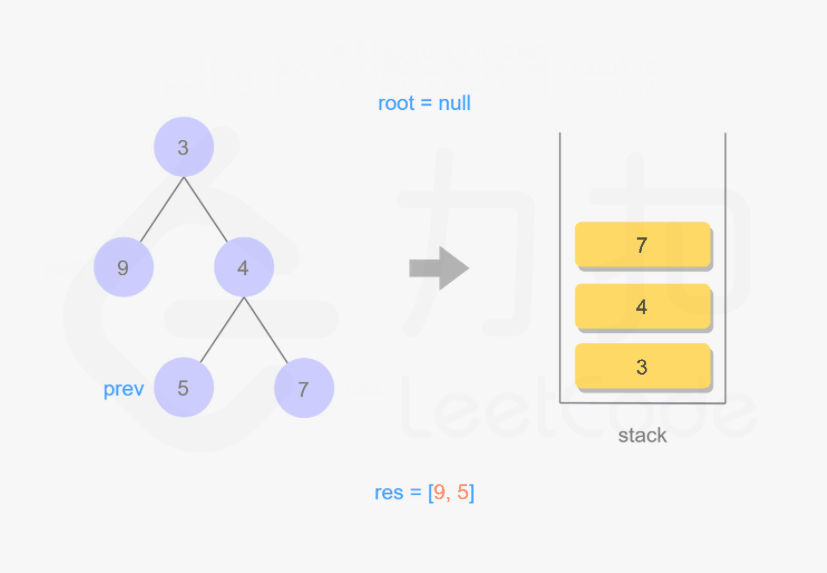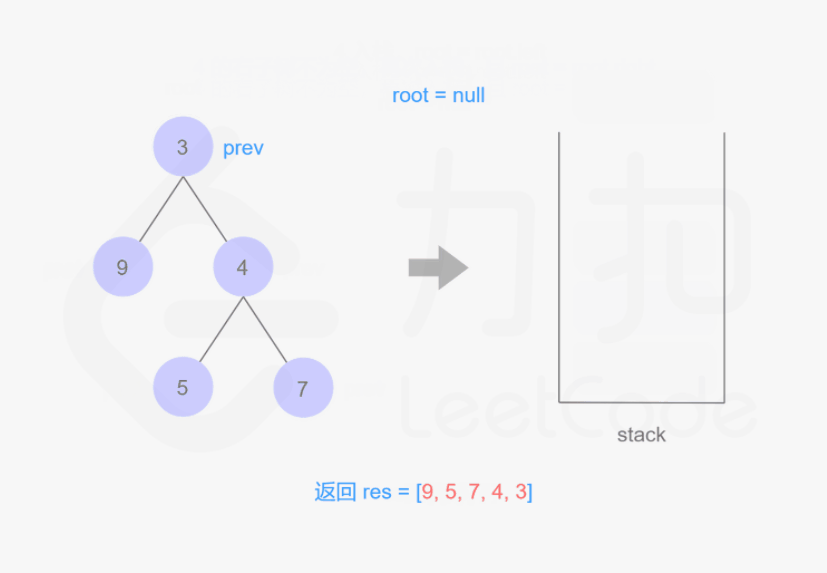
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中n是二叉搜索树的节点数。每一个节点恰好被遍历一次。 - 空间复杂度:
O(n),为迭代过程中显式栈的开销,平均情况下为O(logn),最坏情况下树呈现链状,为O(n)。
方法三:Morris 遍历
思路与算法
有一种巧妙的方法可以在线性时间内,只占用常数空间来实现后序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出,因此被称为 Morris 遍历。
Morris 遍历的核心思想是利用树的大量空闲指针,实现空间开销的极限缩减。其后序遍历规则总结如下:
- 新建临时节点,令该节点为 root;
- 如果当前节点的左子节点为空,则遍历当前节点的右子节点;
如果当前节点的左子节点不为空,在当前节点的左子树中找到当前节点在中序遍历下的前驱节点;
- 如果前驱节点的右子节点为空,将前驱节点的右子节点设置为当前节点,当前节点更新为当前节点的左子节点。
- 如果前驱节点的右子节点为当前节点,将它的右子节点重新设为空。倒序输出从当前节点的左子节点到该前驱节点这条路径上的所有节点。当前节点更新为当前节点的右子节点。
重复步骤 2 和步骤 3,直到遍历结束。
这样我们利用 Morris 遍历的方法,后序遍历该二叉搜索树,即可实现线性时间与常数空间的遍历。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中n是二叉树的节点数。没有左子树的节点只被访问一次,有左子树的节点被访问两次。 - 空间复杂度:
O(1)。只操作已经存在的指针(树的空闲指针),因此只需要常数的额外空间。
102. 二叉树的层序遍历
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例:
二叉树:[3,9,20,null,null,15,7],
1 | 3 |
返回其层序遍历结果:
1 | [ |
方法一:广度优先搜索
思路和算法
我们可以用广度优先搜索解决这个问题。
我们可以想到最朴素的方法是用一个二元组 (node, level) 来表示状态,它表示某个节点和它所在的层数,每个新进队列的节点的 level 值都是父亲节点的 level 值加一。最后根据每个点的 level 对点进行分类,分类的时候我们可以利用哈希表,维护一个以 level 为键,对应节点值组成的数组为值,广度优先搜索结束以后按键 level 从小到大取出所有值,组成答案返回即可。
考虑如何优化空间开销:如何不用哈希映射,并且只用一个变量 node 表示状态,实现这个功能呢?
我们可以用一种巧妙的方法修改广度优先搜索:
- 首先根元素入队
- 当队列不为空的时候
- 求当前队列的长度 s_i
- 依次从队列中取 s_i个元素进行拓展,然后进入下一次迭代
它和普通广度优先搜索的区别在于,普通广度优先搜索每次只取一个元素拓展,而这里每次取 s_i个元素。在上述过程中的第 i 次迭代就得到了二叉树的第 i 层的 s_i个元素。
为什么这么做是对的呢?我们观察这个算法,可以归纳出这样的循环不变式:第 i 次迭代前,队列中的所有元素就是第 i 层的所有元素,并且按照从左向右的顺序排列。证明它的三条性质(你也可以把它理解成数学归纳法):
- 初始化:i=1 的时候,队列里面只有 root,是唯一的层数为 1 的元素,因为只有一个元素,所以也显然满足「从左向右排列」;
- 保持:如果 i=k 时性质成立,即第 k 轮中出队 sk的元素是第 k 层的所有元素,并且顺序从左到右。因为对树进行广度优先搜索的时候由低 k 层的点拓展出的点一定也只能是 k+1 层的点,并且 k+1 层的点只能由第 k 层的点拓展到,所以由这 s_k个点能拓展到下一层所有的 s{k+1} 个点。又因为队列的先进先出(FIFO)特性,既然第 k 层的点的出队顺序是从左向右,那么第 k+1 层也一定是从左向右。至此,我们已经可以通过数学归纳法证明循环不变式的正确性。
- 终止:因为该循环不变式是正确的,所以按照这个方法迭代之后每次迭代得到的也就是当前层的层次遍历结果。至此,我们证明了算法是正确的。
1 | class Solution { |
复杂度分析
记树上所有节点的个数为 n。
- 时间复杂度:每个点进队出队各一次,故渐进时间复杂度为 O(n)。
- 空间复杂度:队列中元素的个数不超过 n 个,故渐进空间复杂度为 O(n)。
104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
1 | 3 |
返回它的最大深度 3 。
方法一:深度优先搜索
思路与算法
如果我们知道了左子树和右子树的最大深度 l 和 r,那么该二叉树的最大深度即为 max(l,r)+1
而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言,在计算当前二叉树的最大深度时,可以先递归计算出其左子树和右子树的最大深度,然后在 O(1) 时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。
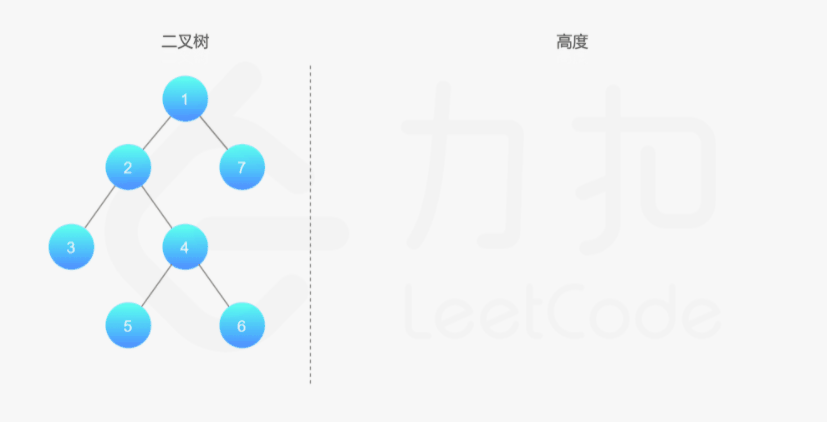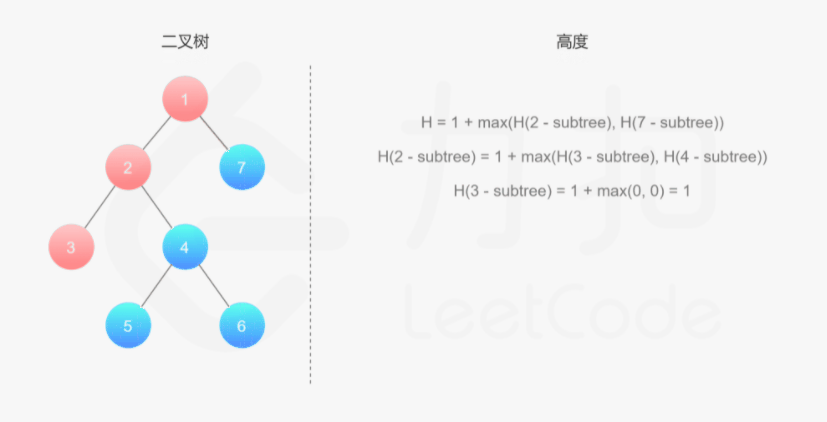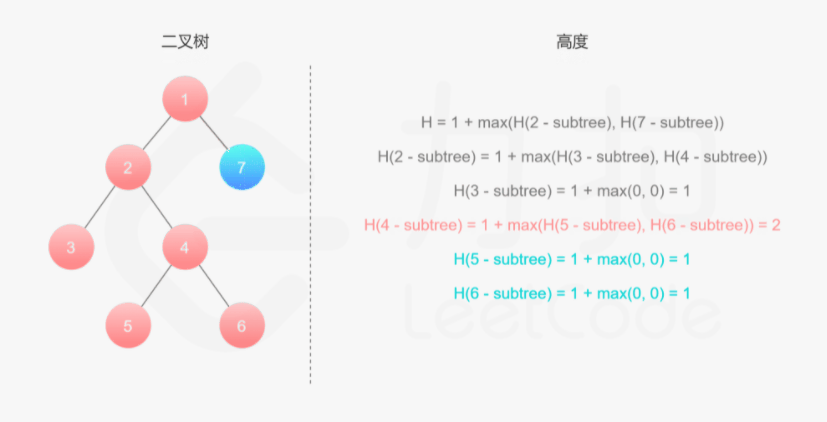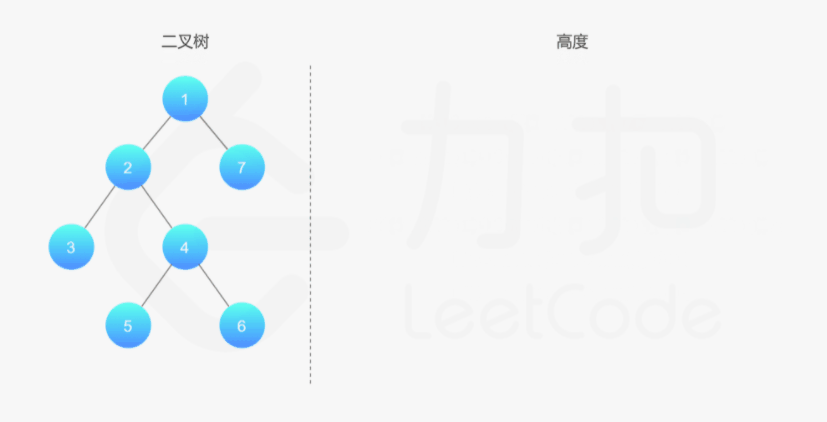
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中n为二叉树节点的个数。每个节点在递归中只被遍历一次。 - 空间复杂度:
O(height),其中height表示二叉树的高度。递归函数需要栈空间,而栈空间取决于递归的深度,因此空间复杂度等价于二叉树的高度。
方法二:广度优先搜索
思路与算法
我们也可以用「广度优先搜索」的方法来解决这道题目,但我们需要对其进行一些修改,此时我们广度优先搜索的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候,不同于广度优先搜索的每次只从队列里拿出一个节点,我们需要将队列里的所有节点都拿出来进行拓展,这样能保证每次拓展完的时候队列里存放的是当前层的所有节点,即我们是一层一层地进行拓展,最后我们用一个变量 ans 来维护拓展的次数,该二叉树的最大深度即为 ans。
1 | class Solution { |
复杂度分析
- 时间复杂度:O(n),其中 n 为二叉树的节点个数。与方法一同样的分析,每个节点只会被访问一次。
- 空间复杂度:此方法空间的消耗取决于队列存储的元素数量,其在最坏情况下会达到 O(n)。
101. 对称二叉树
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1 | 1 |
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1 | 1 |
方法一:递归
思路和算法
如果一个树的左子树与右子树镜像对称,那么这个树是对称的。
因此,该问题可以转化为:两个树在什么情况下互为镜像?
如果同时满足下面的条件,两个树互为镜像:
- 它们的两个根结点具有相同的值
- 每个树的右子树都与另一个树的左子树镜像对称
我们可以实现这样一个递归函数,通过「同步移动」两个指针的方法来遍历这棵树,p 指针和 q 指针一开始都指向这棵树的根,随后 p 右移时,q 左移,pp 左移时,q 右移。每次检查当前 p 和 q 节点的值是否相等,如果相等再判断左右子树是否对称。
1 | class Solution { |
复杂度分析
假设树上一共 n 个节点。
- 时间复杂度:这里遍历了这棵树,渐进时间复杂度为 O(n)。
- 空间复杂度:这里的空间复杂度和递归使用的栈空间有关,这里递归层数不超过 n,故渐进空间复杂度为 O(n)。
方法二:迭代
思路和算法
「方法一」中我们用递归的方法实现了对称性的判断,那么如何用迭代的方法实现呢?首先我们引入一个队列,这是把递归程序改写成迭代程序的常用方法。初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值(队列中每两个连续的结点应该是相等的,而且它们的子树互为镜像),然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时,或者我们检测到树不对称(即从队列中取出两个不相等的连续结点)时,该算法结束。
1 | class Solution { |
复杂度分析
- 时间复杂度:O(n),同「方法一」。
- 空间复杂度:这里需要用一个队列来维护节点,每个节点最多进队一次,出队一次,队列中最多不会超过 n 个点,故渐进空间复杂度为 O(n)。
226. 翻转二叉树
翻转一棵二叉树。
示例:
输入:
1 | 4 |
输出:
1 | 4 |
备注:
这个问题是受到 Max Howell 的 原问题 启发的 :
方法一:递归
思路与算法
这是一道很经典的二叉树问题。显然,我们从根节点开始,递归地对树进行遍历,并从叶子节点先开始翻转。如果当前遍历到的节点 root 的左右两棵子树都已经翻转,那么我们只需要交换两棵子树的位置,即可完成以 root 为根节点的整棵子树的翻转。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(N),其中N为二叉树节点的数目。我们会遍历二叉树中的每一个节点,对每个节点而言,我们在常数时间内交换其两棵子树。 - 空间复杂度:
O(N)。使用的空间由递归栈的深度决定,它等于当前节点在二叉树中的高度。在平均情况下,二叉树的高度与节点个数为对数关系,即O(logN)。而在最坏情况下,树形成链状,空间复杂度为O(N)。
112. 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ,判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。
叶子节点 是指没有子节点的节点。
示例 1:
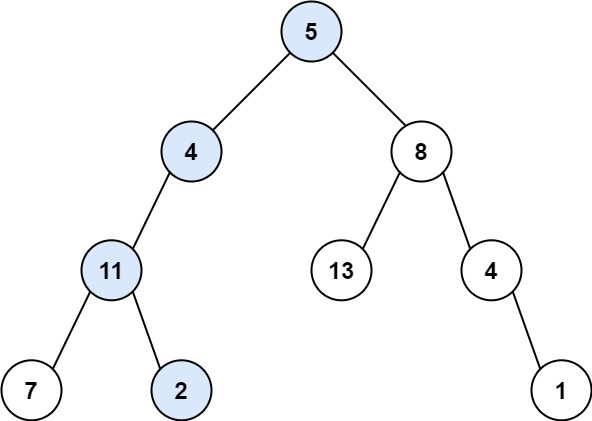
1 | 输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 |
示例 2:
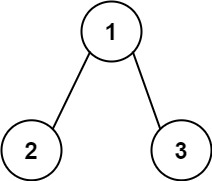
1 | 输入:root = [1,2,3], targetSum = 5 |
示例 3:
1 | 输入:root = [1,2], targetSum = 0 |
提示:
- 树中节点的数目在范围 [0, 5000] 内
- -1000 <=
Node.val<= 1000 - -1000 <=
targetSum<= 1000
注意到本题的要求是,询问是否有从「根节点」到某个「叶子节点」经过的路径上的节点之和等于目标和。核心思想是对树进行一次遍历,在遍历时记录从根节点到当前节点的路径和,以防止重复计算。
需要特别注意的是,给定的 root 可能为空。
方法一:广度优先搜索
思路及算法
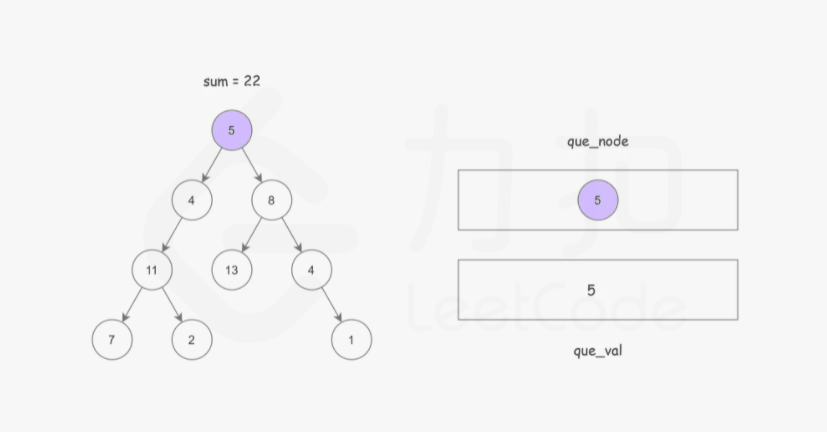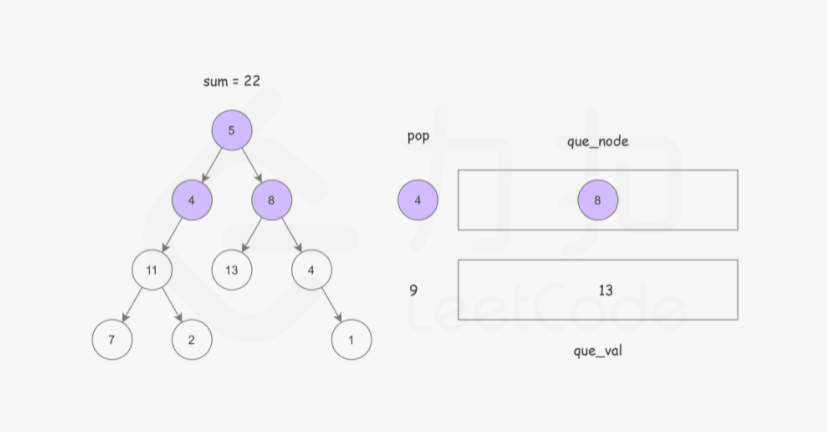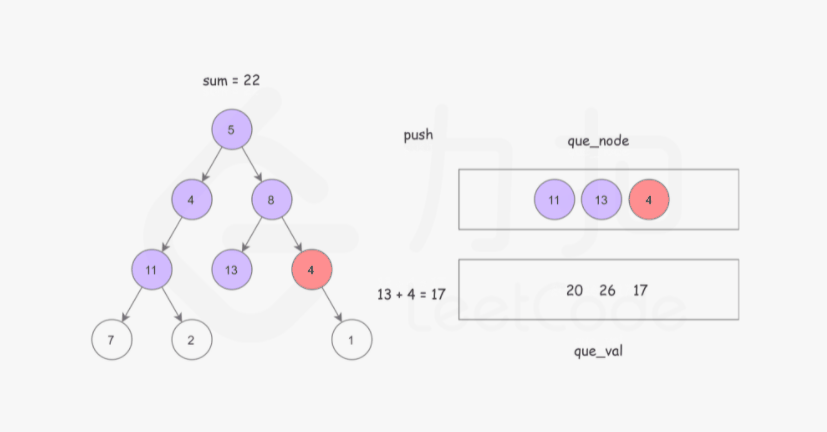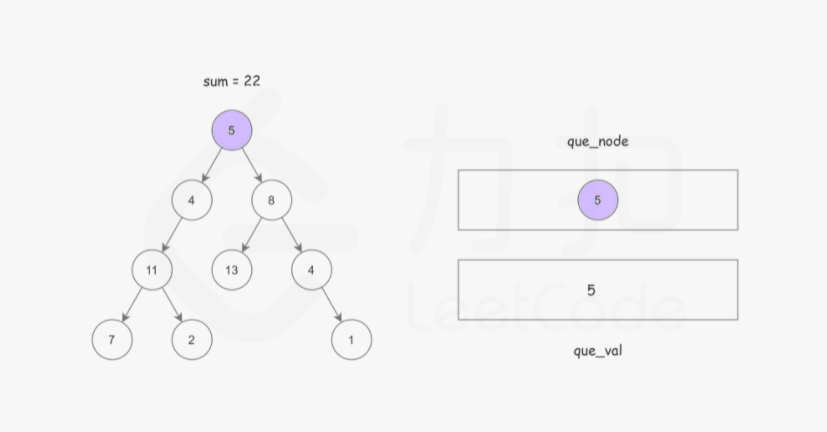
首先我们可以想到使用广度优先搜索的方式,记录从根节点到当前节点的路径和,以防止重复计算。
这样我们使用两个队列,分别存储将要遍历的节点,以及根节点到这些节点的路径和即可。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(N),其中N是树的节点数。对每个节点访问一次。 - 空间复杂度:
O(N),其中N是树的节点数。空间复杂度主要取决于队列的开销,队列中的元素个数不会超过树的节点数。
方法二:递归
思路及算法
观察要求我们完成的函数,我们可以归纳出它的功能:询问是否存在从当前节点 root 到叶子节点的路径,满足其路径和为 sum。
假定从根节点到当前节点的值之和为 val,我们可以将这个大问题转化为一个小问题:是否存在从当前节点的子节点到叶子的路径,满足其路径和为 sum - val。
不难发现这满足递归的性质,若当前节点就是叶子节点,那么我们直接判断 sum 是否等于 val 即可(因为路径和已经确定,就是当前节点的值,我们只需要判断该路径和是否满足条件)。若当前节点不是叶子节点,我们只需要递归地询问它的子节点是否能满足条件即可。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(N),其中N是树的节点数。对每个节点访问一次。 - 空间复杂度:
O(H),其中H是树的高度。空间复杂度主要取决于递归时栈空间的开销,最坏情况下,树呈现链状,空间复杂度为O(N)。平均情况下树的高度与节点数的对数正相关,空间复杂度为O(logN)。
700. 二叉搜索树中的搜索
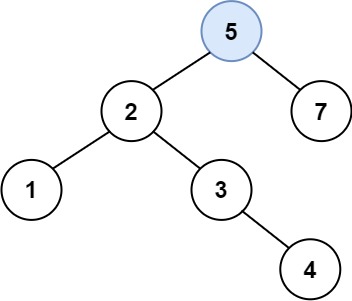
给定二叉搜索树(BST)的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 NULL。
例如,
1 | 给定二叉搜索树: |
你应该返回如下子树:
1 | 2 |
在上述示例中,如果要找的值是 5,但因为没有节点值为 5,我们应该返回 NULL。
二叉搜索树
二叉搜索树是一棵二叉树,每个节点都有以下特性:
- 大于左子树上任意一个节点的值,
- 小于右子树上任意一个节点的值。
一个二叉搜索树的例子:
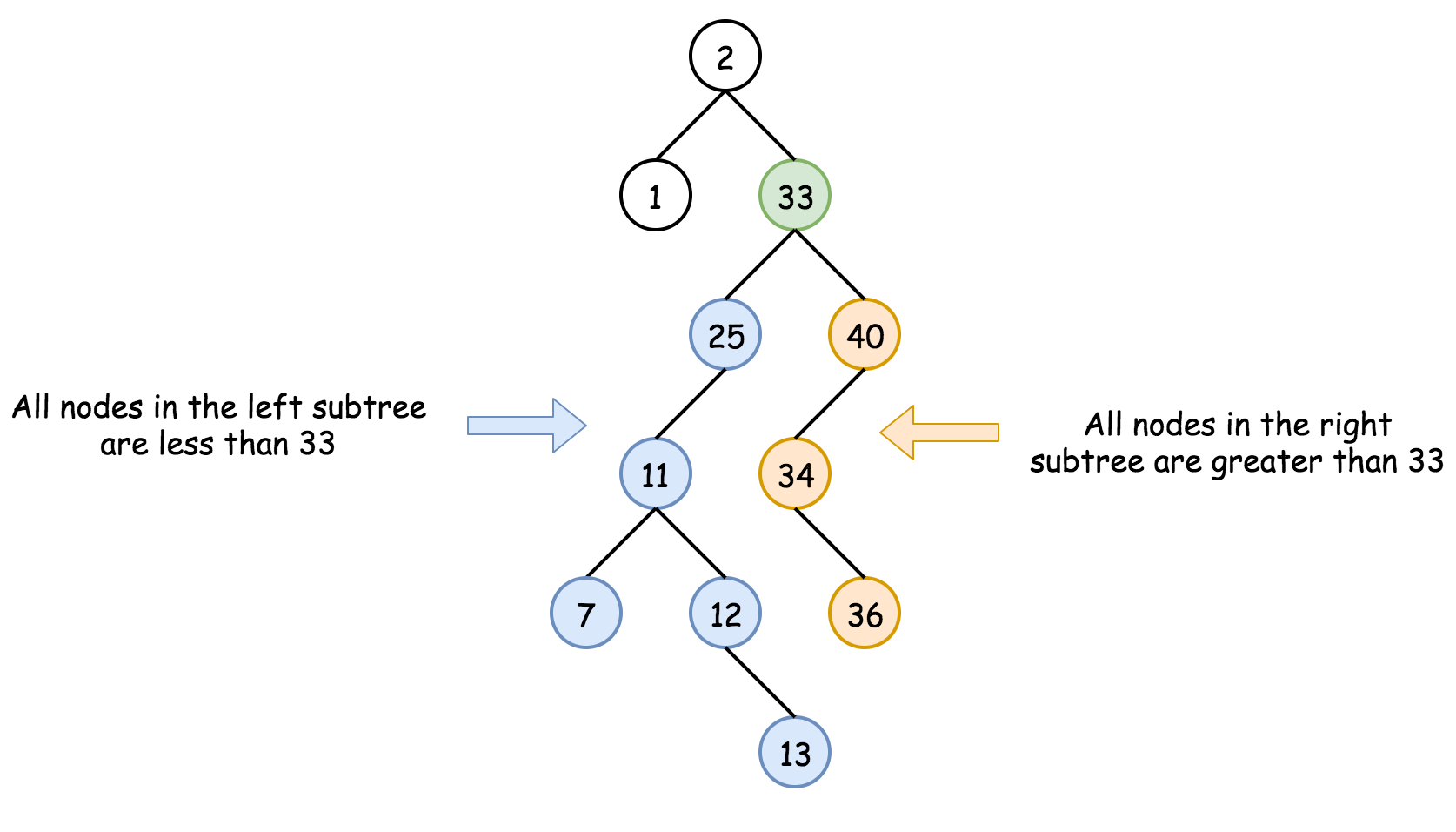
二叉搜索树中复杂度为对数时间的操作:
方法一:递归
算法
递归实现非常简单:
- 如果根节点为空 root == null 或者根节点的值等于搜索值 val == root.val,返回根节点。
- 如果 val < root.val,进入根节点的左子树查找 searchBST(root.left, val)。
- 如果 val > root.val,进入根节点的右子树查找 searchBST(root.right, val)。
- 返回根节点。
1 | class Solution { |

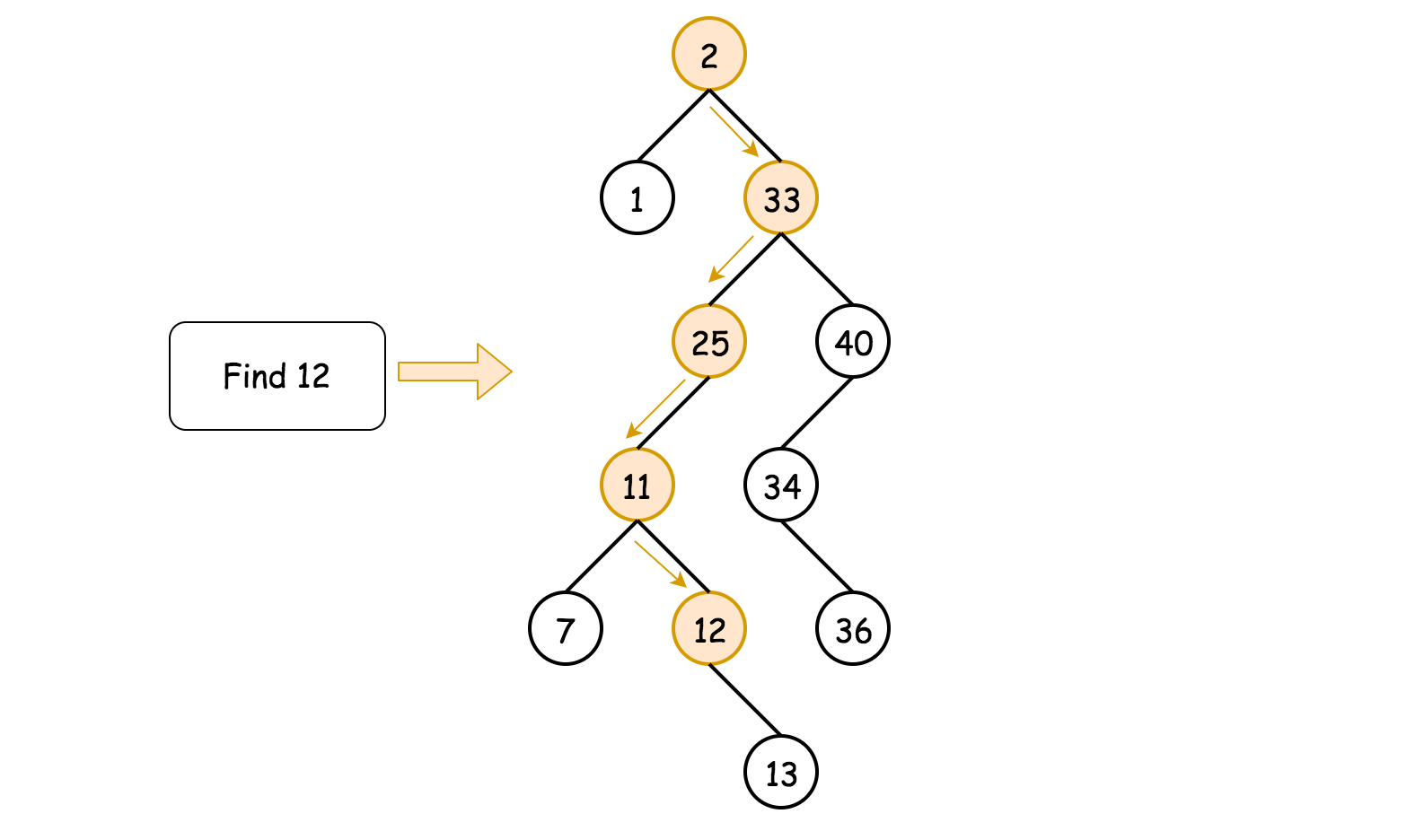
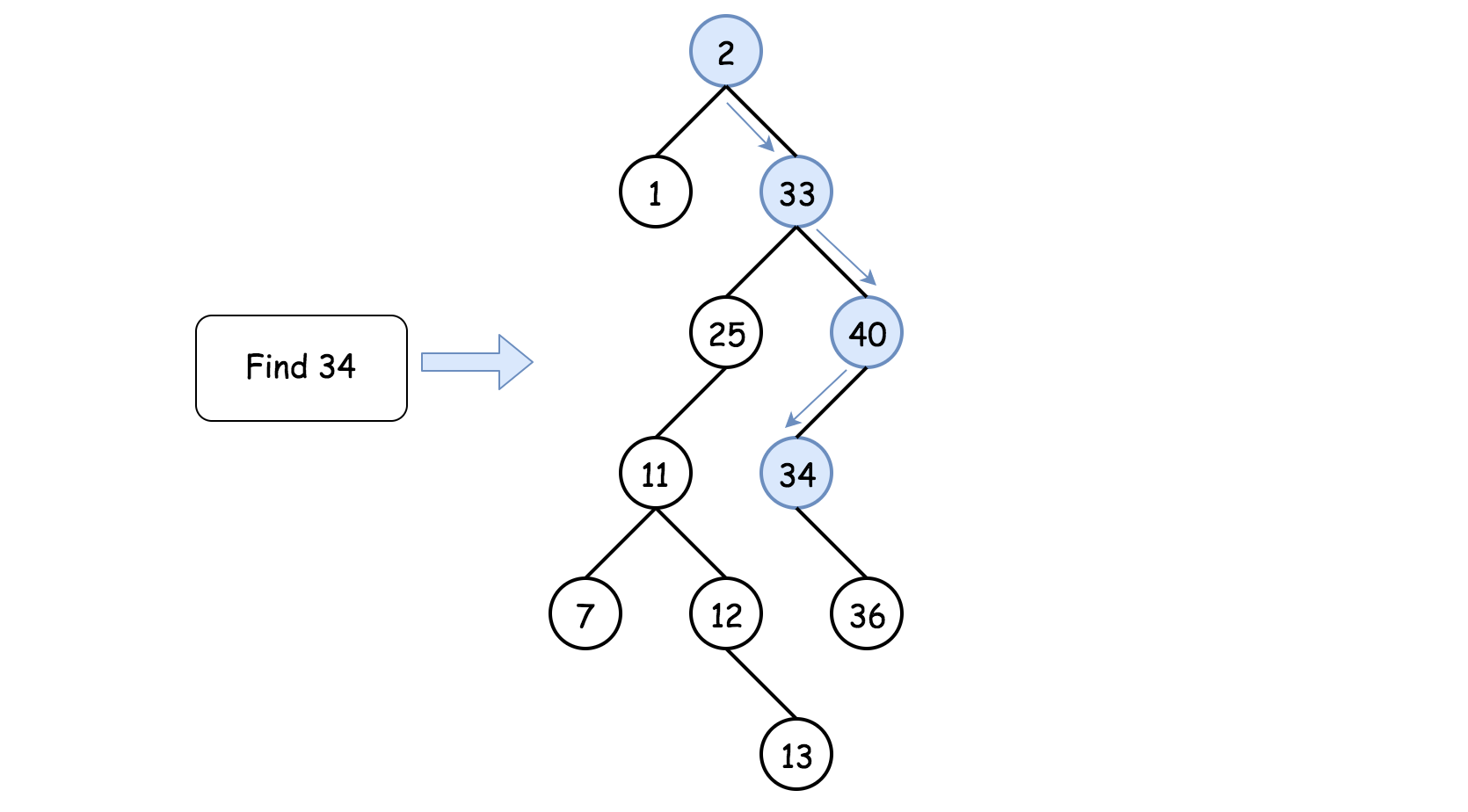
方法二:迭代
为了降低空间复杂度,将递归转换为迭代:
如果根节点不空 root != null 且根节点不是目的节点 val != root.val:
- 如果 val < root.val,进入根节点的左子树查找 root = root.left。
- 如果 val > root.val,进入根节点的右子树查找 root = root.right。
返回 root。
1 |
|

701. 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点和要插入树中的值,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
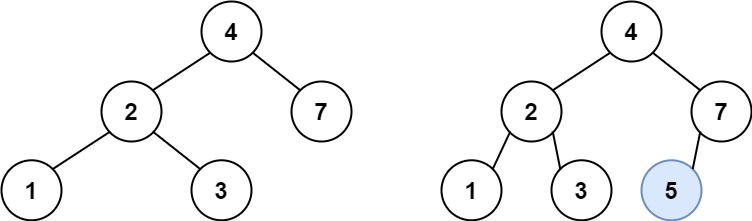
1 | 输入:root = [4,2,7,1,3], val = 5 |
示例 2:
1 | 输入:root = [40,20,60,10,30,50,70], val = 25 |
示例 3:
1 | 输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 |
提示:
- 给定的树上的节点数介于 0 和 10^4 之间
- 每个节点都有一个唯一整数值,取值范围从 0 到 10^8
- -10^8 <= val <= 10^8
- 新值和原始二叉搜索树中的任意节点值都不同
方法一:模拟
思路与算法

1 | class Solution { |
复杂度分析
- 时间复杂度:
O(N),其中N为树中节点的数目。最坏情况下,我们需要将值插入到树的最深的叶子结点上,而叶子节点最深为O(N)。 - 空间复杂度:
O(1)。我们只使用了常数大小的空间。
98. 验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
1 | 输入: |
示例 2:
1 | 输入: |
方法一: 递归

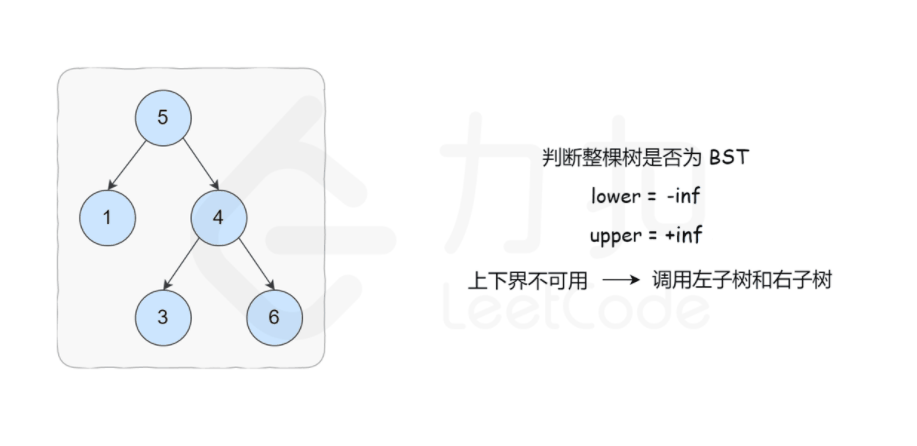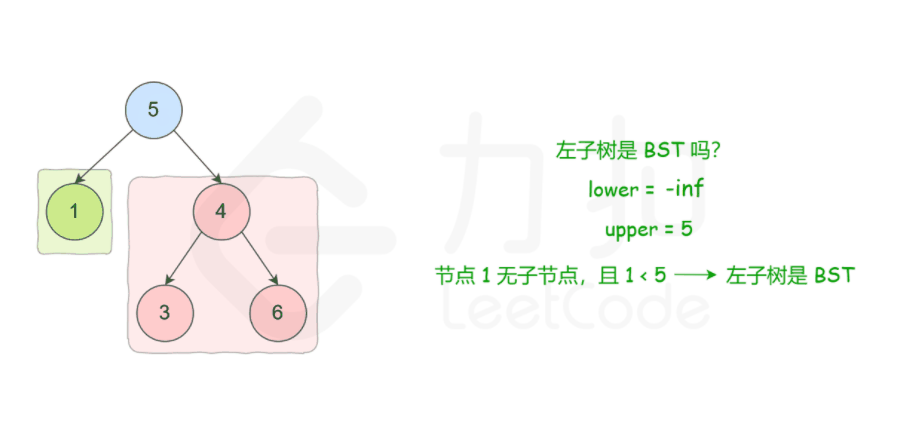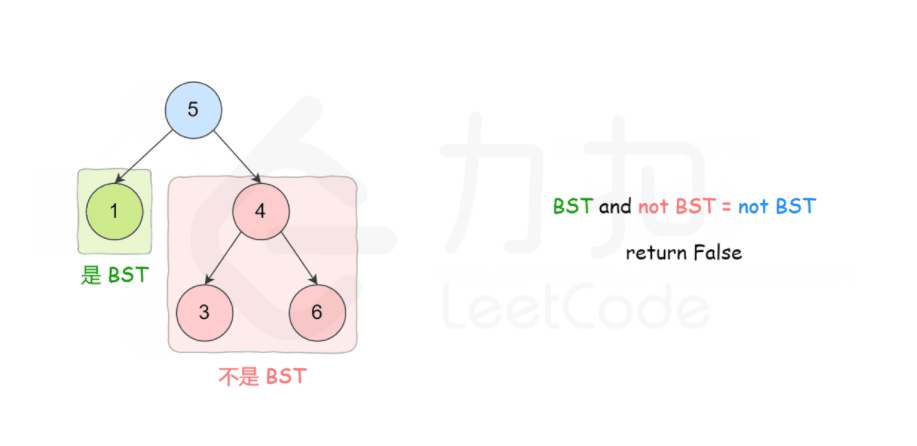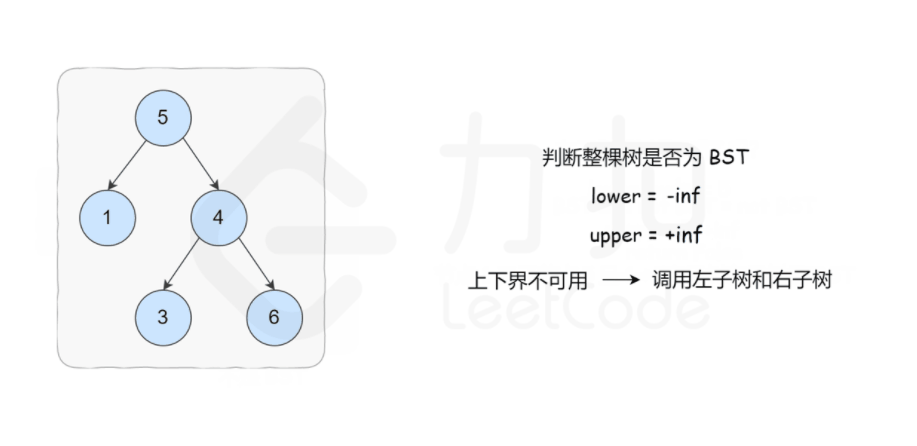
1 | class Solution { |

方法二:中序遍历

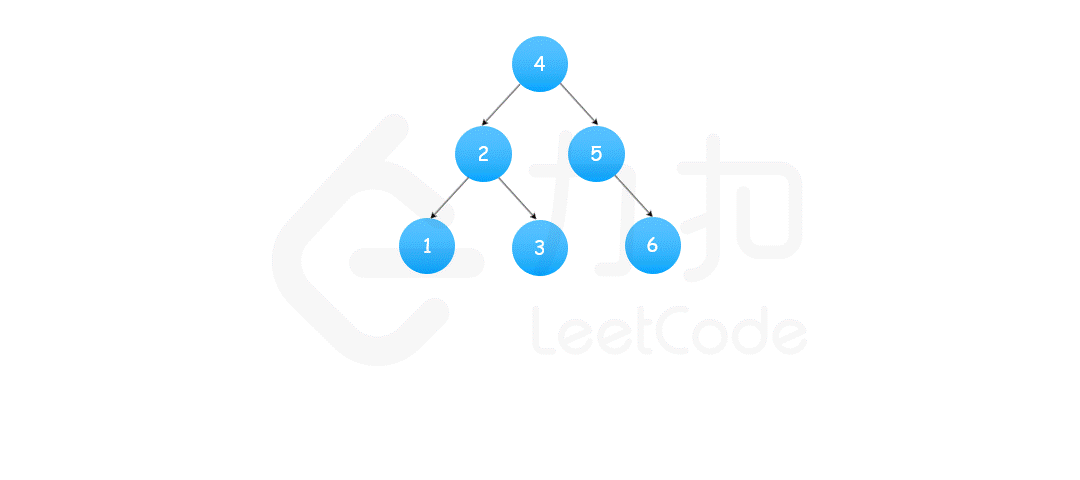
1 | class Solution { |
复杂度分析
- 时间复杂度 :
O(n),其中n为二叉树的节点个数。二叉树的每个节点最多被访问一次,因此时间复杂度为O(n)。 - 空间复杂度 :
O(n),其中n为二叉树的节点个数。栈最多存储n个节点,因此需要额外的O(n)的空间。
653. 两数之和 IV - 输入 BST
给定一个二叉搜索树 root 和一个目标结果 k,如果 BST 中存在两个元素且它们的和等于给定的目标结果,则返回 true。
示例 1:
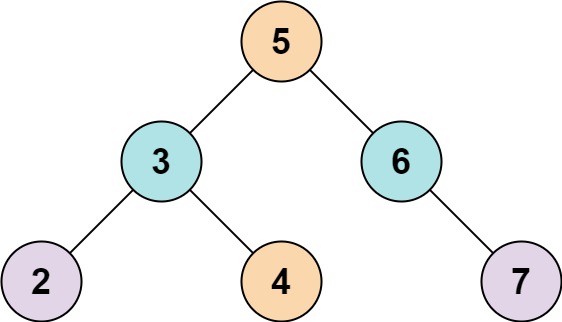
1 | 输入: root = [5,3,6,2,4,null,7], k = 9 |
示例 2:
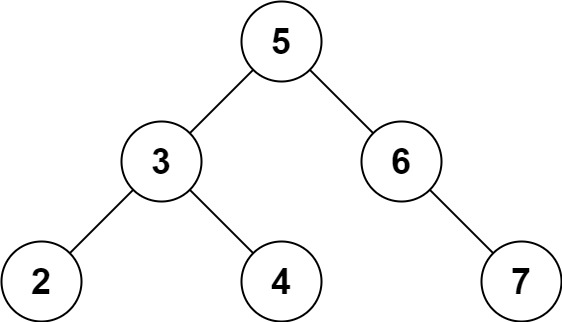
1 | 输入: root = [5,3,6,2,4,null,7], k = 28 |
示例 3:
1 | 输入: root = [2,1,3], k = 4 |
示例 4:
1 | 输入: root = [2,1,3], k = 1 |
示例 5:
1 | 输入: root = [2,1,3], k = 3 |
提示:
- 二叉树的节点个数的范围是 [1, 104].
- -104 <= Node.val <= 104
- root 为二叉搜索树
- -105 <= k <= 105
方法一:使用 HashSet【通过】
最简单的方法就是遍历整棵树,找出所有可能的组合,判断是否存在和为 k 的一对节点。现在在此基础上做一些改进。
如果存在两个元素之和为 k,即 x+y=k,并且已知 xx 是树上一个节点的值,则只需判断树上是否存在一个值为 y 的节点,使得 y=k-x。基于这种思想,在树的每个节点上遍历它的两棵子树(左子树和右子树),寻找另外一个匹配的数。在遍历过程中,将每个节点的值都放到一个 set 中。
对于每个值为 p 的节点,在 set 中检查是否存在 k−p。如果存在,那么可以在该树上找到两个节点的和为 k;否则,将 p 放入到 set 中。
如果遍历完整棵树都没有找到一对节点和为 k,那么该树上不存在两个和为 k 的节点
1 | public class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中N是节点的数量。最坏的情况下,整棵树被遍历一次。 - 空间复杂度:
O(n)。最坏的情况下,set 存储 n 个节点的值。
方法二:使用 BFS 和 HashSet【通过】
算法
本方法中,set 的用途与 方法一 相同。但是本方法使用广度优先搜索遍历二叉树,这是一种非常常见的遍历方法。
使用广度优先搜索查找一对节点和为 k 的过程如下。首先维护一个与 方法一 用途相同的 set。将根节点加入 queue,然后执行以下步骤:
- 从队列首部删除一个元素 p。
- 检查 set 中是否存在 k−p。如果存在,返回 True。
- 否则,将 p 加入 set。然后将当前节点的左孩子和右孩子加入 queue。
- 重复步骤一至三,直到 queue 为空。
- 如果 queue 为空,返回 False。
按照以上步骤,逐层遍历二叉树。
1 | public class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中 n 是树中节点的数量。最坏的情况下,需要遍历整棵树。 - 空间复杂度:
O(n)。最坏的情况下,set 存储 n 个节点的值。
方法三:使用 BST【通过】
算法
在本方法中利用 BST 的性质,BST 的中序遍历结果是按升序排列的。因此,中序遍历给定的 BST,并将遍历结果存储到 list 中。
遍历完成后,使用两个指针 l 和 r 作为 list 的头部索引和尾部索引。然后执行以下操作:
检查 l 和 r 索引处两元素之和是否等于 k。如果是,立即返回 True。
如果当前两元素之和小于 k,则更新 l 指向下一个元素。这是因为当我们需要增大两数之和时,应该增大较小数。
如果当前两元素之和大于 k,则更新 r 指向上一个元素。这是因为当我们需要减小两数之和时,应该减小较大数。
重复步骤一至三,直到左指针 l 大于右指针 r。
如果左指针 l 到右指针 r 的右边,则返回 False。
注意,在任何情况下,都不应该增大较大的数,也不应该减小较小的数。这是因为如果当前两数之和大于 k,不应该首先增大 list[r] 的值。类似的,也不应该首先减小 list[l] 的值。
1 | public class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中 n 是树中节点的数量。本方法需要中序遍历整棵树。 - 空间复杂度:
O(n),list 中存储 n 个元素。
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
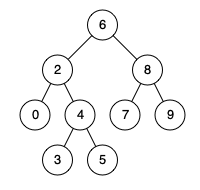
示例 1:
1 | 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 |
示例 2:
1 | 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 |
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
方法一:两次遍历
思路与算法
注意到题目中给出的是一棵「二叉搜索树」,因此我们可以快速地找出树中的某个节点以及从根节点到该节点的路径,例如我们需要找到节点 p:
我们从根节点开始遍历;
如果当前节点就是 p,那么成功地找到了节点;
如果当前节点的值大于 p 的值,说明 p 应该在当前节点的左子树,因此将当前节点移动到它的左子节点;
如果当前节点的值小于 p 的值,说明 p 应该在当前节点的右子树,因此将当前节点移动到它的右子节点。
对于节点 q 同理。在寻找节点的过程中,我们可以顺便记录经过的节点,这样就得到了从根节点到被寻找节点的路径。

1 | class Solution { |

方法二:一次遍历
思路与算法
在方法一中,我们对从根节点开始,通过遍历找出到达节点 p 和 q 的路径,一共需要两次遍历。我们也可以考虑将这两个节点放在一起遍历。
整体的遍历过程与方法一中的类似:
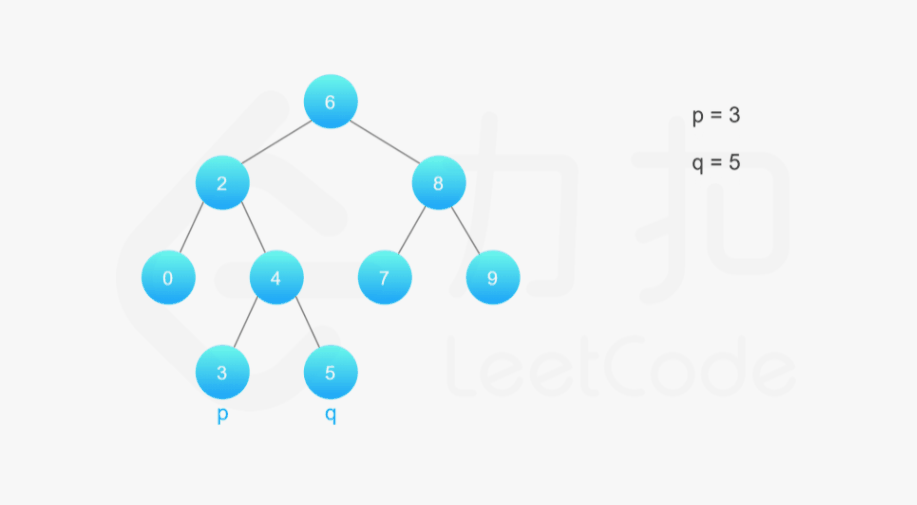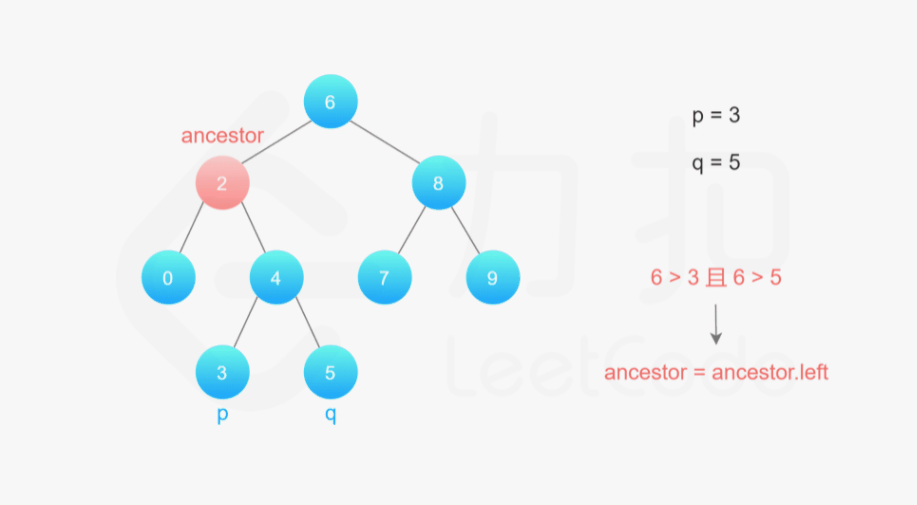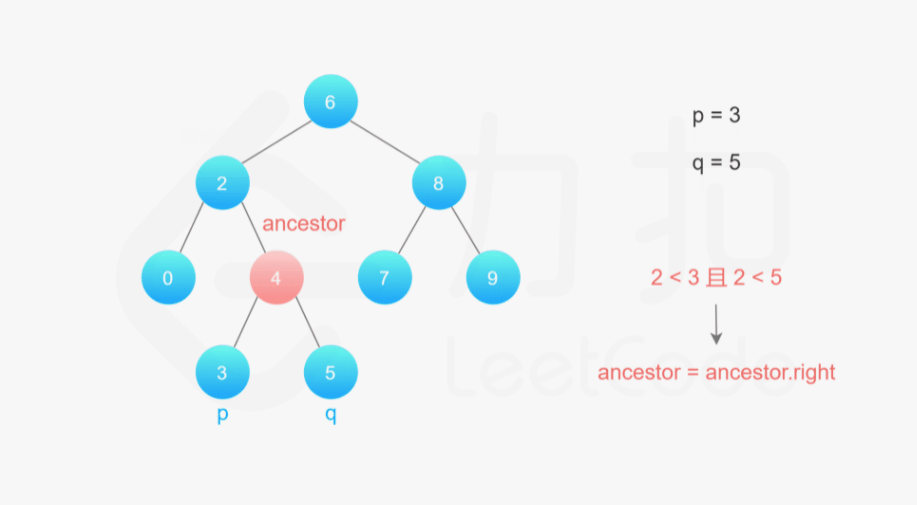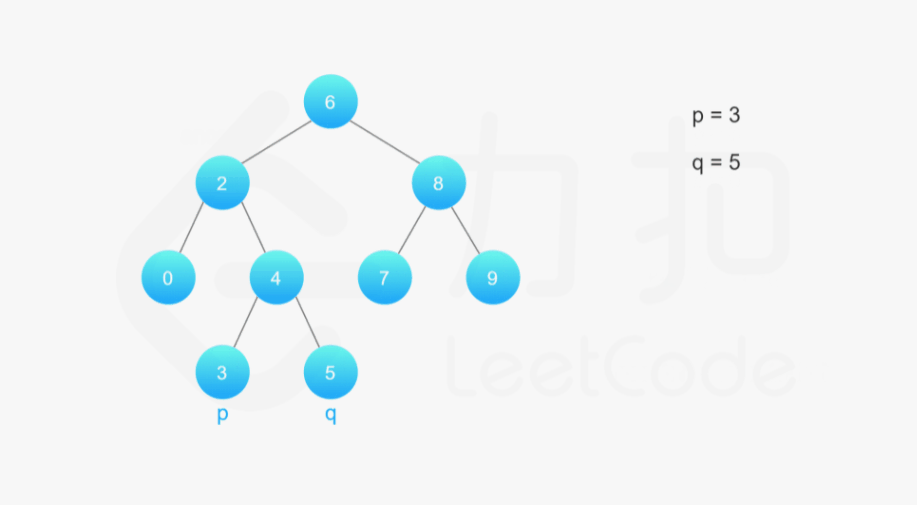
- 我们从根节点开始遍历;
- 如果当前节点的值大于 p 和 q 的值,说明 p 和 q 应该在当前节点的左子树,因此将当前节点移动到它的左子节点;
- 如果当前节点的值小于 p 和 q 的值,说明 p 和 q 应该在当前节点的右子树,因此将当前节点移动到它的右子节点;
- 如果当前节点的值不满足上述两条要求,那么说明当前节点就是「分岔点」。此时,p 和 q 要么在当前节点的不同的子树中,要么其中一个就是当前节点。
可以发现,如果我们将这两个节点放在一起遍历,我们就省去了存储路径需要的空间。
1 | class Solution { |
复杂度分析
- 时间复杂度:
O(n),其中n是给定的二叉搜索树中的节点个数。分析思路与方法一相同。 - 空间复杂度:
O(1)。
...
...
Copyright 2021 sunfy.top ALL Rights Reserved