一、位运算符
Java中支持的位运算符
&:按位与
| 操作数1 |
操作数2 |
& |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
总结:只有两个操作数都为1时,按位与操作的结果才为1,否则为0。(有0结果就为0)
|:按位或
| 操作数1 |
操作数2 |
\ |
|
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
总结:只要两个操作数中有一个为1,按位或的结果就为1,否则为0。(有1结果就为1)
~:按位非
| 操作数1 |
操作数2 |
^ |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
总结:两个操作数相异则为1,相同则为0。
<<:左移
符号位不变,低位补0.
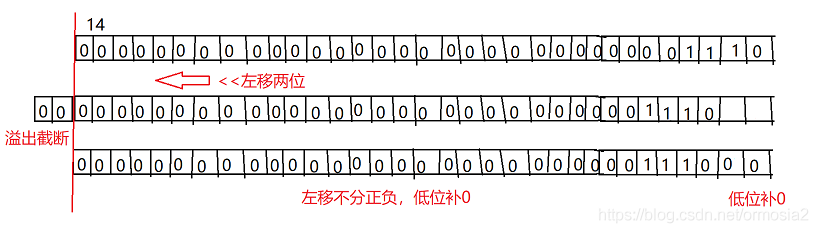
>>: 右移
低位溢出,符号位不变,高位溢出补符号位.
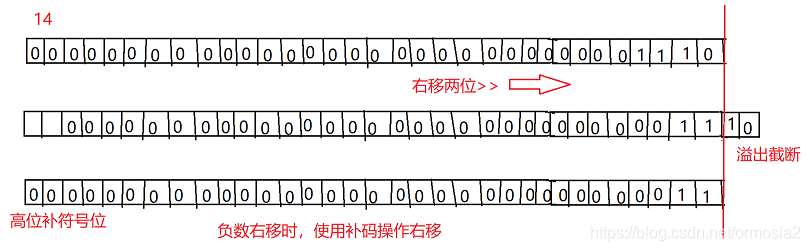
>>>: 无符号右移
低位溢出,高位补0。无符号为的意思就是把符号位当作数字位看待.
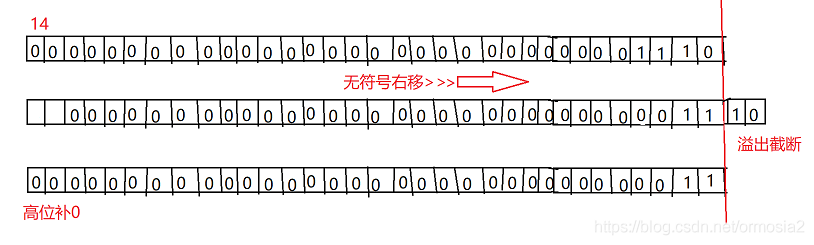
二、使用位运算符解决问题
1、求一个整数的二进制表示中1的个数
最常用的方法就是/2 ,%2法,其实我们还可以通过位运算符>>>和&来解决这个问题
1
2
| 我们知道&运算符,只有在两个操作数都是1的情况下结果才为1.那么我们可以让该数>>>(无符号右移) 同时 &上1
只要>>>后的数不为0,就一直& 1
|
1
2
3
4
5
6
7
8
9
10
| public static void fun(int n) {
int count = 0;
while(n != 0) {
if((n & 1) != 0) {
count++;
}
n = n >>> 1;
}
System.out.println(count);
}
|
上述方法并不是最优,我们还可以用另外一种方法:
1
2
3
4
5
6
7
8
| public static void fun(int n) {
int count = 0;
while(n != 0) {
count++;
n = n & (n - 1);
}
System.out.peintln(count);
}
|
2、分别输出一个整数二进制表示的奇数位序列和偶数位序列
1
2
3
4
5
6
7
8
| public static void fun(int n) {
for(int i = 31;i >= 0;i -= 2) {
System.out.println(((n >> i) & 1) + " ");
}
for(int i = 30;i >= 0;i -= 2) {
System.out.peintln(((n >> i) & 1 ) + " ");
}
}
|
3、一组数据中,有一个数据只出现了一次,其他数据都出现了两次,求只出现一次的数据是哪个
1
2
3
4
5
6
7
| public static void fun(int[] array) {
int res = 0;
for(int i = 0;i < array.length;i++) {
res = res ^ array[i];
}
System.out.peintln(res);
}
|
三、位运算符与加减运算符之间的关系及实际运用。
关系:位运算符比加减运算符运算速度更快。一般能用位运算的就用位运算符。
实际运用:
实例1:输入一个整数,输出该数二进制表示中1的个数,如:9的二进制表示是1001,有2位是1,因此如果输入9,该函数输出2.
| 输入 |
二进制表示 |
输出 |
| 9 |
0000 0000 0000 0000 0000 0000 0000 1001 |
2 |
第一种思路:使用 >> 运算符,将数据右移,不断与数字 1做与 & 运算,若与运算结果为1,则该位置二进制表示为1,否则为0;
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public class Test {
public static void main(String[] args)
{
int a=9;
System.out.println("数字 "+a+" 在内存中得二进制表示为:"+Integer.toBinaryString(a)+
" 二进制表示法包含的位数是:"+ getNumOf1(a));
}
public static int getNumOf1(int n)
{
int number=0;
while(n!=0)
{
if ((n&1)==1)
number++;
n=n>>1;
}
return number;
}
}
|
程序执行结果:
1
2
| 数字 9 在内存中得二进制表示为:1001 二进制表示法包含的位数是:2
Process finished with exit code 0
|
问题:
存在问题,移位运算中,当n时正数时,右移的话,最左面补0
正值>> 左面补0 负值>> 左面补1 正负<< 右面补0
在本段代码中,当a是负数时,右移的话,最左面补位补的是1,一直右移就一直补1.会造成死循环 (1000)>>(1100)>>(1110)>>(1111)>>…>>1111。思考:有没有什么方法,让正负数 在 >> 操作时,左面均补位0 ? 答案: >>> 操作。
另外,如果我们首先判断数据是否是负值,负值的话,将数据变为相反数,即正值再判断1的个数,这种方法是不可取的,因为在内存中数据存储的是补码。不是源码。我们判断的是数据的补码中 1 出现的次数。将数据变为相反数后,数据在内存中表示,不止符号位发生变化,数据位也发生变化。
第二种思路:使用 >>> 运算符,将数据右移,不断与数字 1做与 & 运算,若与运算结果为1,则该位置二进制表示为1,否则为0;
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public class Test {
public static void main(String[] args)
{
int a=9;
int b=-9;
System.out.println("数字 "+a+" 在内存中得二进制表示为:"+Integer.toBinaryString(a)+
" 二进制表示法包含的位数是:"+ getNumOf1(a));
System.out.println("数字 "+b+" 在内存中得二进制表示为:"+Integer.toBinaryString(b)+
" 二进制表示法包含的位数是:"+ getNumOf1(b));
}
public static int getNumOf1(int n)
{
int number=0;
while(n!=0)
{
if ((n&1)==1)
number++;
n=n>>>1;
}
return number;
}
}
|
程序执行结果:
1
2
3
| 数字 9 在内存中得二进制表示为:1001 二进制表示法包含的位数是:2
数字 -9 在内存中得二进制表示为:11111111111111111111111111110111 二进制表示法包含的位数是:31
Process finished with exit code 0
|
第三种思路:使用 << 运算符,flag=1,将flag左移,不断与数字 n做与 & 运算,若与运算结果不为0,则该位置二进制表示为1,否则为0直至flag为0;
这里红色字体:与运算结果不为0。与运算结果情况有两种
与数据位 & ,结果大于0;
与符号位 & ,若数据是负数,即符号位为1,则与结果- 2147483648(写个实例看看为何是这个数字),即: 是负数 ,若数据是正数,即符号位为0,则与结果为0。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public class Test {
public static void main(String[] args)
{
int a=9;
int b=-9;
System.out.println("数字 "+a+" 在内存中得二进制表示为:"+Integer.toBinaryString(a)+
" 二进制表示法包含的位数是:"+ getNumOf1(a));
System.out.println("数字 "+b+" 在内存中得二进制表示为:"+Integer.toBinaryString(b)+
" 二进制表示法包含的位数是:"+ getNumOf1(b));
}
public static int getNumOf1(int n)
{
int flag=1;
int number=0;
while(flag!=0)
{
if((flag&n) != 0)
number++;
flag=flag<<1;
}
return number;
}
}
|
程序执行结果:
1
2
3
| 数字 9 在内存中得二进制表示为:1001 二进制表示法包含的位数是:2
数字 -9 在内存中得二进制表示为:11111111111111111111111111110111 二进制表示法包含的位数是:31
Process finished with exit code 0
|
第四种思路:有没有什么方法,只在1出现时计算,0时不计算?
对于任意数据n,n-1操作是将n的二进制表示中,最右面的1变为0,且最右面1的后面部分全取反。n=n & (n-1),则是将n的二进制表示中,最右面的1的后面全变为0。利用这一特性,统计二进制表示中1的个数。
| n |
n-1 |
n=n & (n-1) |
二进制表示中1出现的次数 |
| 11 - 0001 0011 |
10 - 0001 0010 |
10 - 0001 0010 |
1 |
| 10 - 0001 0010 |
9 - 0001 0001 |
8 - 0001 0000 |
2 |
| 8 - 0001 0000 |
7- 0000 1111 |
0 - 0000 0000 |
3 |
| 0 - 0000 0000 |
结束 |
|
3 |
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public class Test {
public static void main(String[] args)
{
int a=9;
int b=-9;
System.out.println("数字 "+a+" 在内存中得二进制表示为:"+Integer.toBinaryString(a)+
" 二进制表示法包含的位数是:"+ getNumOf1(a));
System.out.println("数字 "+b+" 在内存中得二进制表示为:"+Integer.toBinaryString(b)+
" 二进制表示法包含的位数是:"+ getNumOf1(b));
}
public static int getNumOf1(int n)
{
int number=0;
while(n!=0)
{
number++;
n=n&(n-1);
}
return number;
}
}
|
程序执行结果:
1
2
3
| 数字 9 在内存中得二进制表示为:1001 二进制表示法包含的位数是:2
数字 -9 在内存中得二进制表示为:11111111111111111111111111110111 二进制表示法包含的位数是:31
Process finished with exit code 0
|
其他应用:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
public static boolean is2(int number)
{
if((number&(number-1))==0)
return true;
return false;
}
public static int Getn(int m,int n)
{
int dif=m^n;
int number=0;
while(dif!=0)
{
number++;
dif=dif&(dif-1);
}
return number;
}
public static int add(int num1, int num2) {
int sum = 0;
while (num2 != 0) {
sum = (num1 ^ num2);
num2 = (num1 & num2) << 1;
num1 = sum;
}
return num1;
}
n>>1;
n<<1;
|



Copyright 2021 sunfy.top ALL Rights Reserved