PriorityBlockingQueue

PriorityBlockingQueue是一个无界的基于数组的优先级阻塞队列，数组的默认长度是11，虽然指定了数组的长度，但是可以无限的扩充，直到资源消耗尽为止，每次出队都返回优先级别最高的或者最低的元素。默认情况下元素采用自然顺序升序排序，当然我们也可以通过构造函数来指定Comparator来对元素进行排序。需要注意的是PriorityBlockingQueue不能保证同优先级元素的顺序。

优先级队列PriorityQueue： 队列中每个元素都有一个优先级，出队的时候，优先级最高的先出。

一个支持优先级排序的无界阻塞队列：优先级高的先出队，优先级低的后出队

数据结构：数组+二叉堆：默认容量11，可指定初级容量，会自动扩容，最大容量是（Integer.MAX_VALUE - 8）

锁：ReentrantLock：存取是同一把锁

阻塞对象：NotEmpty：出队，队列为空时阻塞

入队：

• 不阻塞，永远返回成功，无界
• 根据比较器进行堆化（排序）自上而下
  • 传入比较器对象就按照比较器的顺序排序
  • 传入比较器对象就按照比较器的顺序排序

出队：

• 优先级最高的元素在堆顶（弹出堆顶元素）
• 弹出前比较两个子节点再进行堆化（自上而下）

应用场景：

• 业务办理排队叫号，VIP客户插队
• 电商抢购活动，会员级别高的用户优先抢购到商品

使用

1
2
3
4
5
6
7
8
9
10

//创建优先级阻塞队列  Comparator为null,自然排序
PriorityBlockingQueue<Integer> queue=new PriorityBlockingQueue<Integer>(5);
//自定义Comparator
PriorityBlockingQueue queue=new PriorityBlockingQueue<Integer>(
        5, new Comparator<Integer>() {
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2-o1;
    }
});

如何实现一个优先级队列？

如何构造优先级队列

使用普通线性数组(无序)来表示优先级队列

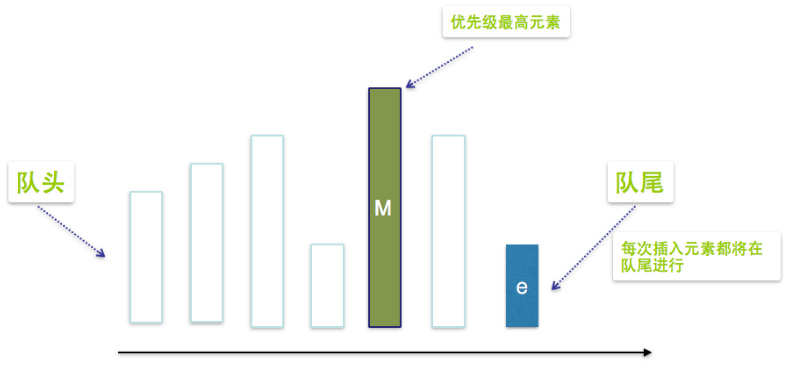
• 执行插入操作时，直接将元素插入到数组末端，需要的成本为O(1),
• 获取优先级最高元素，我们需要遍历整个线性队列，匹配出优先级最高元素，需要的成本为o(n)
• 删除优先级最高元素，我们需要两个步骤，第一找出优先级最高元素，第二步删除优先级最高元素，然后将后面的元素依次迁移，填补空缺，需要的成本为O(n)+O(n)=O(n)

使用一个按顺序排列的有序向量实现优先级队列

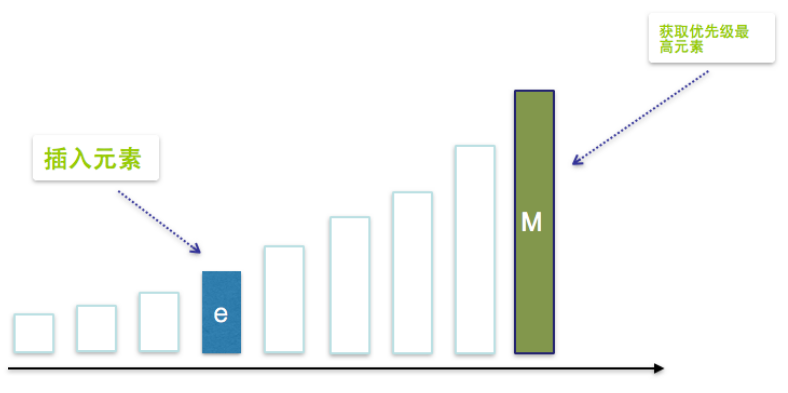
• 获取优先级最高元素，O(1)
• 删除优先级最高元素，O(1)
• 插入一个元素，需要两个步骤，第一步我们需要找出要插的位置，这里我们可以使用二分查找，成本为O(logn)，第二步是插入元素之后，将其所有后继进行后移操作，成本为O(n)，所有总成本为O(logn)+O(n)=O(n)

二叉堆

完全二叉树：除了最后一行，其他行都满的二叉树，而且最后一行所有叶子节点都从左向右开始排序。

二叉堆：完全二叉树的基础上，加以一定的条件约束的一种特殊的二叉树。根据约束条件的不同，二叉堆又可以分为两个类型：

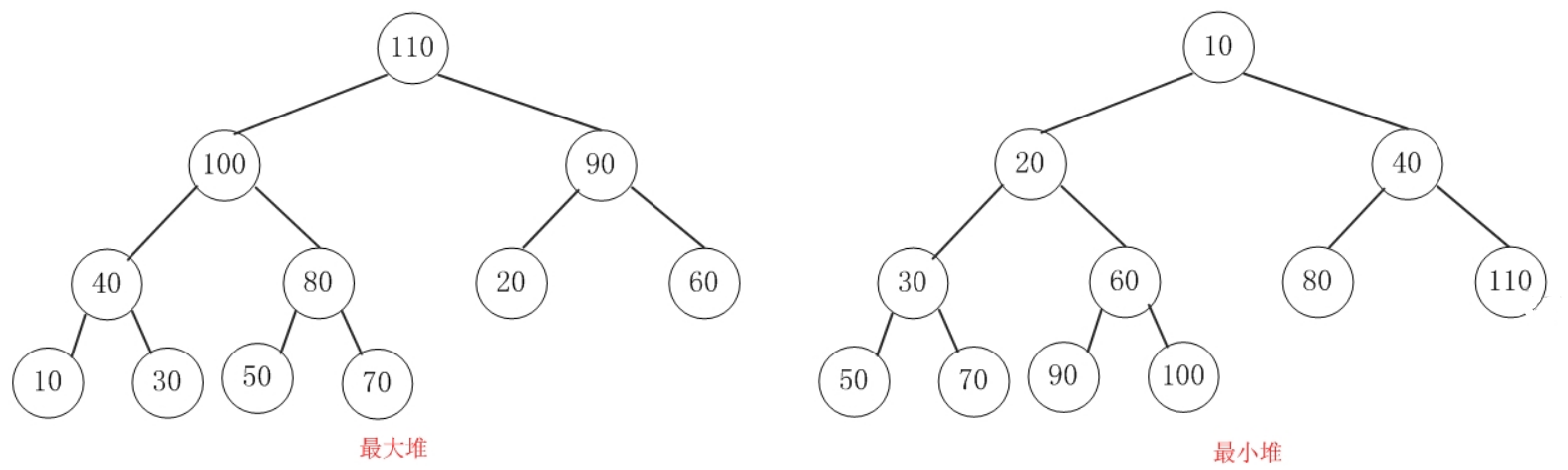
大顶堆和小顶堆。

• 大顶堆（最大堆）：父结点的键值总是大于或等于任何一个子节点的键值；
• 小顶堆（最小堆）：父结点的键值总是小于或等于任何一个子节点的键值。

• ← Previous Post
• Next Post →

...

...

00:00

00:00